Ângulos externos de um polígono convexo
Soma dos ângulos externos
Observe as applets a seguir e verifique o que ocorre quando unimos os ângulos externos de um polígono convexo pelos vértices.
Triângulo (Adaptado de produção de Derivando a Matemática)
Quadrilátero (Adaptado de produção de Derivando a Matemática)
Pentágono (Adaptado de produção de Derivando a Matemática)
Que ângulo foi gerado pela união dos ângulos externos dos polígonos verificados?
Ampliação e formalização do pensamento
Observamos que todos os polígonos verificados têm a soma de seus ângulos externos igual a um ângulo de volta completa, ou seja, 360º.
O que pode nos levar a supor que esse padrão será sempre verdadeiro.
Vamos agora realizar a demonstração dessa relação.
Demonstração
Observando um ângulo externo (representado em verde) e o ângulo interno adjacente (representado em azul) podemos perceber que juntos formam um ângulo raso, ou seja, um ângulo de 180°
Polígono (dodecágono)
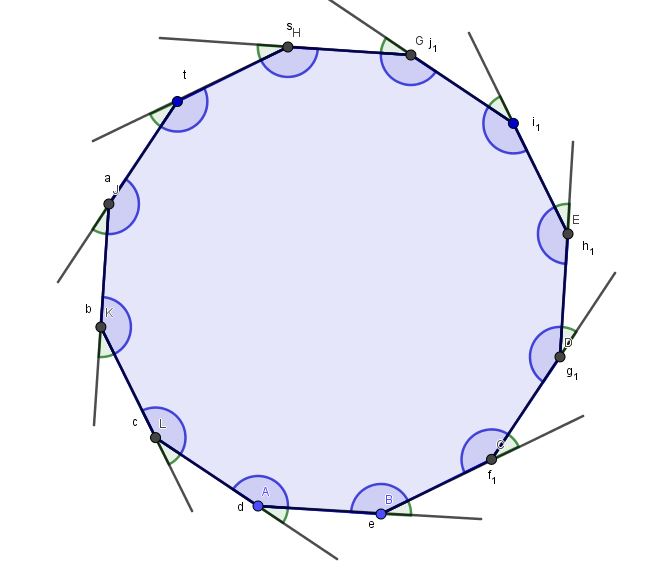
Assim, se nosso objetivo fosse somar todos os ângulos internos e externos, poderíamos dizer que a soma seria , pois, para cada vértice, teríamos um ângulo raso.
Como já sabemos que a soma dos ângulos internos é .
Então, se
Ângulos externos + Ângulos internos =
Ângulos externos +
Ângulos externos =
Ângulos externos =
Ângulos externos =
Podemos, então, concluir que em qualquer polígono convexo a soma dos ângulos externos será 360°.