Interunion-Euclidean
Interunion a ⋇ b is the act of spinning fibers into threads. In the simplest case, two fibers are spun into an epicycloid thread (check "Quadratic" to restrict all cases into epicycloid) or a hypocycloid (check both "Qradratic" & "Spatial"). In the general case, from the initial two fibers a & b, they are refined into many "remainder" fibers ri via Euclidean algorithm, and then all of them are spun together into a complex thread via partial Fourier series of those fibers. In that partial Fourier series, all harmonics are synchronized with a constant velocity (c = 1), i.e. wavelength = period = amplitude × 2π = 2π·ri, so that those harmonics are touching circles together spinning a high-order cycloid thread (epicycloid & hypocycloid are 2-cycloids, cycloid & circle are 1-cycloids).
See the following images for comparison between epicycloid/hypocycloid (left) and complex (right) threads:
Epicycloid versus complex thread for 12⋇5 = {12, 5, 2, 1}
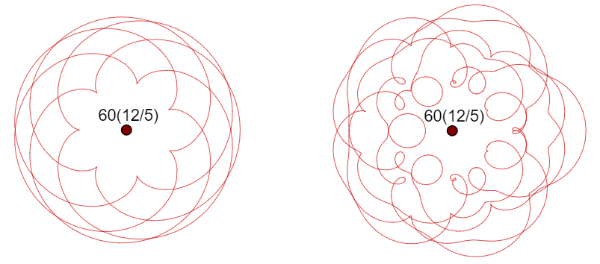
Hypocycloid versus complex thread for 12⋇-5 = {12, -5, 2, -1}
Let R := set of remainders, including a & b, and Nr = |R|, e.g. R = {12, -7, 5, 2, -1, 1}, Nr = 6.
The (extensional) product thread is an Nr-cycloid projected from the trace of Nr-D phase vector which is a diagonal line wrapping around and filling the hyper-box Nr-orthotope, as shown in the "Linear box" (only 2-box) in the applet. From Chinese remainder theorem, we have the extent (period) of that line = LCM(R).
When LCM(R) > LCM(a, b), e.g. 420 > 84, we have the Nr-cycloid longer than the corresponding quadratic 2-cycloid.
Epicycloid versus complex thread for 12⋇7 = {12, 7, 5, 2, 1}

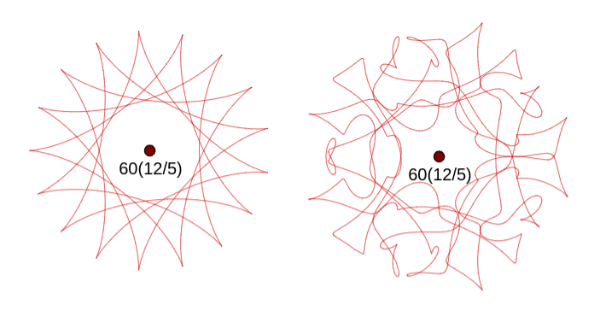
Hypocycloid versus complex thread for 12⋇-7 = {12, -7, 5, -2, 1, -1}
