Our Pedagogical Framework
Pedagogical Framework for Teaching Integral Calculus
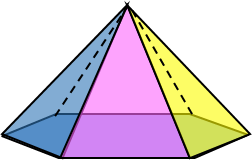
We propose a pedagogical framework of six questions that illustrates what secondary math teachers need to know and teach calculus effectively. The framework is based on prior research, theories, and practices. We envision a three-dimensional figure, a hexagonal pyramid with the six knowledge types as the vertices of the base, and students' learning as the top vertex. Arrows point from each vertex to every other vertex symbolizing reciprocity. Teachers must know how to answer every question to show that they are effective math teachers and possess deep knowledge of calculus.
- What? Teachers must know their subject with its concepts and facts. They must know how to solve mathematical problems. They also need to possess a frame of reference in which they teach math.
- Who? To teach effectively, a teacher must be familiar with the students' background: prior knowledge, family background, age, hobbies, conception, misconception, etc. Any students' characteristics that might help or hinder students in their learning.
- How? Teachers must know what makes the learning of specific topics easy or difficult. A teacher can teach a concept in a mathematically correct way yet "lose" all the students. It is also critical to take students' previous knowledge and misconceptions into consideration when teaching new concepts. Formative assessment and immediate feedback land in this category. If done well, constructive feedback is one of the highest-yielding strategies in raising students' performance.
- Where? Lateral knowledge and vertical knowledge are central to teaching. Teachers not only must know what is taught three grade levels or math courses below and above their level of teaching, but they must also be familiar with what their students are learning in other courses. This element might offer a fertile ground for teacher collaboration, cross-curricular teaching, and research.
- When? The knowledge of "when" entails the goal of teaching with understanding and teaching for transfer. It means that teachers must have the future in mind, not simply strive for immediate results. If teachers teach for understanding, students can expand their knowledge beyond the narrow context they initially learned. We cannot teach every problem to the students; they must see the similarities among the problems and transfer prior knowledge to new, novel situations.
- Why? This question brings us back to the first idea of our framework at a narrower frame: the goal of education at an individual teachers' level. In simple words, we want our students to succeed. We want to instill the love of learning and knowledge in them to become what they dream of becoming.