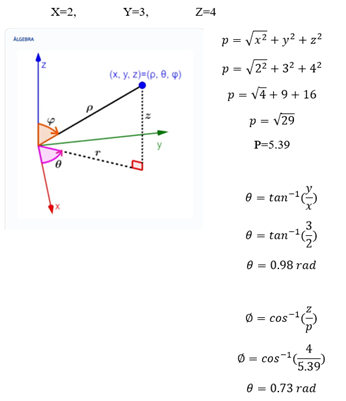
Transformación de coordenadas esféricas a cartesianas y viceversa.
Las coordenadas esféricas poseen la manera (ρ, θ, φ), en donde, ρ es la distancia a partir de los principios hasta el punto, θ es el ángulo en el plano xy con respecto al eje x y φ es el ángulo con respecto al eje z. Estas coordenadas tienen la posibilidad de ser transformadas a coordenadas cartesianas utilizando triángulos rectángulos y trigonometría
1. Tenemos al punto (10,π/4,π/4)en coordenadas esféricas. ¿Cuál es su equivalencia en coordenadas cartesianas?

Tenemos al punto (10,π/4,4π/3)en coordenadas esféricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
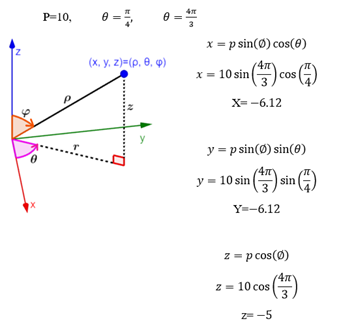
Las coordenadas esféricas son escritas en la manera (ρ, θ, φ), en donde, ρ representa a la distancia a partir de los principios hasta el punto, θ representa al ángulo con respecto al eje x en el plano xy y φ representa al ángulo conformado con respecto al eje z. Las coordenadas esféricas tienen la posibilidad de ser útiles al instante de graficar esferas u otras figuras tridimensionales representadas por ángulos. Este sistema de coordenadas es especialmente eficaz en el cálculo debido a que principalmente resulta más simple obtener las derivadas o integrales utilizando este sistema una vez que poseemos inconvenientes involucrados a esferas o figuras semejantes. Después, aprenderemos las fórmulas que tenemos la posibilidad de utilizar para cambiar de coordenadas cartesianas a esféricas. Después, utilizaremos estas fórmulas para solucionar ciertos ejercicios de práctica.
3. Tenemos al punto (2, 3, 4) en coordenadas cartesianas. ¿Cuál es su equivalencia en coordenadas esféricas?