Google Classroom谷歌课堂
GeoGebraGeoGebra 教室
GeoGebra

Einführung Krümmung

作者:Teacher Weitkamp, Katharina
主题:导数
Das Steigungsverhalten einer Funktion hast du schon mit der ersten Ableitung erkundet. In diesem Abschnitt geht es um das KRÜMMUNGSVERHALTEN einer Funktion. Wir unterscheiden
  • Linkskrümmig (Fachwort: konvex)
  • Rechtskrümmig(Fachwort: konkav)
Wir stellen uns vor, dass der Graph einer Funktion das Profil einer Strasse ist, die in positiver Richtung von links nach rechts durchfahren wird. Ein Graph heißt in einem bestimmten x-Bereich linkskrümmig , wenn der Fahrer beim Durchfahren das Lenkrad nach links dreht, und rechtskrümmig , wenn der Fahrer das Lenkrad nach rechts dreht. (Das ist natürlich nur eine Modellvorstellung). Betrachte das obige Applet. Bediene den Schieberegler. Beantworte anschliessend die Fragen

Der Graph ist im x-Bereich [-10;0] ...

选择所有适用项
  • A
  • B
检查答案 (3)

Der Graph ist im x-Bereich [0;10] ...

选择所有适用项
  • A
  • B
检查答案 (3)

Der Graph ist im x-Bereich [-4,5;4,5] ...

选择所有适用项
  • A
  • B
  • C
检查答案 (3)

Gib ein weiteres Intervall aus dem x-Bereich an, w der Graph rechtskrümmig ist

Betrachte jetzt die zweite Ableitung f'' der Funktion. Die zweite Ableitung gibt das Steigungsverhalten der ersten Ableitung wieder. Welches Vorzeichen haben die Werte der zweiten Ableitung im Krümmungsbereich [-10;0]?

选择所有适用项
  • A
  • B
  • C
检查答案 (3)

Welches Vorzeichen haben die Werte der zweiten Ableitung im Krümmungsbereich [0;10]?

选择所有适用项
  • A
  • B
  • C
检查答案 (3)

Bedeutung der 2.Ableitung - Lies und notiere!

Bedeutung der 2.Ableitung - Lies und notiere!
Lies und notiere!

Graphenpuzzle

Dargestellt sind die Graphen von Funktionen (blau) und ihren zweiten Ableitungen. Ordne die Graphen zu!
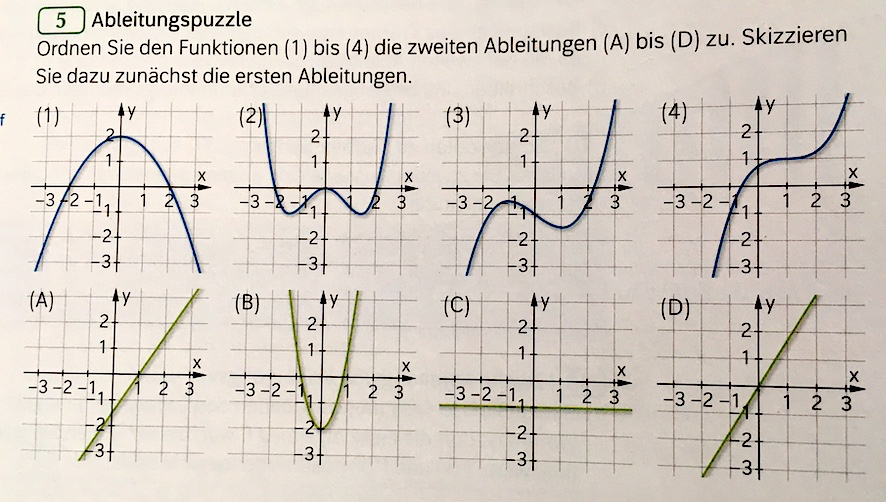
Image

Graph (1) gehört zu

选择所有适用项
  • A
  • B
  • C
  • D
检查答案 (3)

Graph (2) gehört zu

选择所有适用项
  • A
  • B
  • C
  • D
检查答案 (3)

Graph (3) gehört zu

选择所有适用项
  • A
  • B
  • C
  • D
检查答案 (3)

Graph (4) gehört zu

选择所有适用项
  • A
  • B
  • C
  • D
检查答案 (3)

2.Ableitung bilden

Gegeben ist die Funktion g(x)=x^3 +x²+5. Bilde die 2.Ableitung! Anleitung: Bilde die erste Ableitung f'(x) und bilde anschließend die Ableitung der Ableitung (zweimaliges Ableiten) Symbolisch: f''(x)=(x^3+x²+5)''

选择所有适用项
  • A
  • B
  • C
检查答案 (3)

2.Ableitung bilden

Gegeben ist die Funktion g(x)=3x^4 -x^3+5x. Bilde die 2.Ableitung!

选择所有适用项
  • A
  • B
  • C
检查答案 (3)

Krümmungsbereiche ermitteln

1) Bilde die 2.Ableitung 2) Bestimme - falls vorhanden - die Nullstellen der 2.Ableitung 3) Erstelle eine Vorzeichentabelle für die 2.Ableitung (nutze hierfür wieder Teststellen)

Wahr oder falsch?

Wahr oder falsch? Die zweite Ableitung einer Potenzfunktion in der Form f(x)=ax^6 ist wieder eine Potenzfunktion mit Potenzanteil x^4

选择所有适用项
  • A
  • B
检查答案 (3)
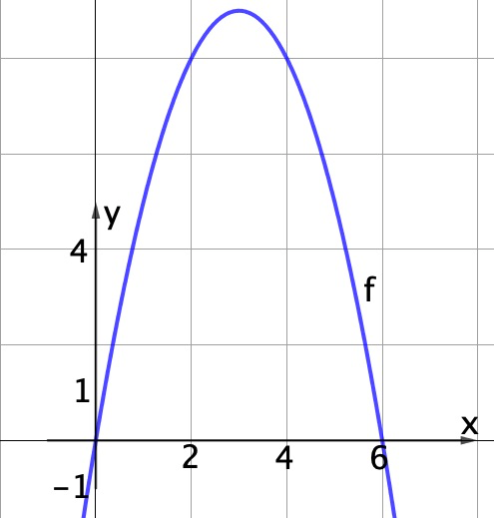
Image

2.Ableitung und Krümmung

Das Schaubild zeigt den Graphen der Funktion f(x)=-x² +6x. Wie du siehst, ist der Graph rechtskrümmig. Bilde die zweite Ableitung und überprüfe, dass f''(x) negative Wert für alle reellen Zahlen x annimmt. Anleitung: Schritt 1: f'(x)=_________________ , f''(x)=___________________ Schritt 2: Vorzeichen der Konstante der 2.Ableitung notieren Antwortsatz: das Vorzeichen der Konstante ist ______________, die Funktion besitzt einen rechtskrümmigen Graph

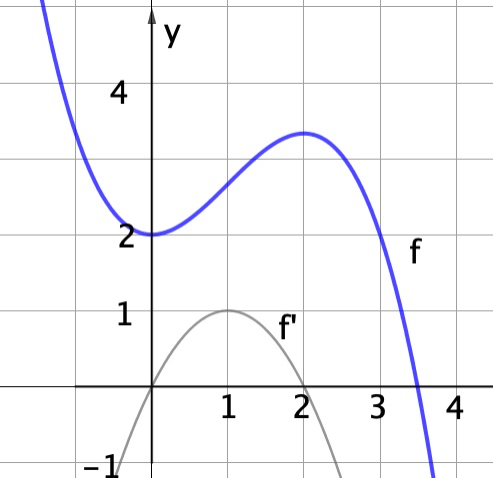
Image

2. Ableitung und Krümmung (Beispiel 2)

Das Schaubild zeigt den Graphen der Funktion f(x)=-1/3 x^3 +x²+2 . Du siehst, dass der Graph auf dem Bereich ]-∞;1] rechtskrümmig und auf dem Bereich [1;+∞[ linkskrümmig ist. Überprüfe! Anleitung: Schritt 1: f'(x)= ______________________ , f''(x)=__________________________ (Ableitungen bilden) Schritt 2: Nullstellen bestimmen: f''(x)= _______________________ = 0 (Nullstellengleichung aufstellen) Lösung x=______________ (1) Schritt 3: Vorzeichentabelle für f''(x) erstellen linke Teststelle wählen x_L=_______, f''(____)=______ (Vorzeichen notieren) rechte Teststelle wählen x_R=_________, f''(____)=________ (Vorzeichen notieren) Antwortsatz aufschreiben

新资源

发现资源

发现主题