Límite de una sucesión
Una secuencia {} converge a un número real si para todo existe un entero tal
que si . El número es el límite de la secuencia y escribimos
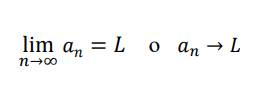
en este caso, decimos que la secuencia {} es una secuencia convergente. Si una secuencia no converge, es una secuencia divergente y decimos que el límite no existe. Observamos que la convergencia o divergencia de una secuencia {} depende solo de lo que sucede con los términos cuando . Por lo tanto, si un número finito de términos , …, se colocan antes de para crear una nueva secuencia. ... al a2, .... ,
esta nueva secuencia convergerá si {} converge y divergirá si {} diverge. Además, si la
secuencia {} converge a , esta nueva secuencia también convergerá a .
Si una secuencia {} no es convergente, decimos que es una secuencia divergente. En la definición informal del límite de una secuencia, usamos los términos “arbitrariamente cerca” y “suficientemente grande”. Aunque estas frases ayudan a ilustrar el significado de una secuencia convergente, son algo vagas. Para ser más precisos, ahora presentamos la definición más formal de límite para una secuencia