H 06 Mi mennyi?
Kapitány a gépháznak:
- Mennyi?
- Nyolcvan!
- Mi nyolcvan?
- Mi mennyi?
Köszöntő
A fenti - talán tapintatlan - régi viccel és egy közös fejtörésünk felidézésével köszöntöm itt és most örökifjú barátomat Németh József Tanár urat (nagy T) az iménti számmal jelzett születésnapja alkalmából.
Kedves Jóskám! Sok szeretettel köszöntelek, megjegyezve, hogy a születésnapok jó hatással vannak az ember egészségére, ezért továbbra is igyekezzünk belőlük minél többet összegyűjteni. :-)
Régi-régi barátsággal:
Szilassi Lajos
Szembe jött az utcán...
A szép matematikai problémák - ha nem is jönnek szembe az utcán - többnyire mégsem tudjuk őket kikerülni. Talán azért, mert nem is nagyon szeretnénk.
Egyszer szembe jött I. F. Sharygin cikke: (Quantum July/August 1998, p.:33-37) A cikk a bemutatott feladatok "megoldásait" is tartalmazza. Hamarosan kiderül, mi indokolja az idézőjelet.
Ebben a cikkben több szép geometriai probléma is jött szembe, bár az alábbi nem tartozik ezek közé.
Mégsem tudtunk kitérni előle. :-)
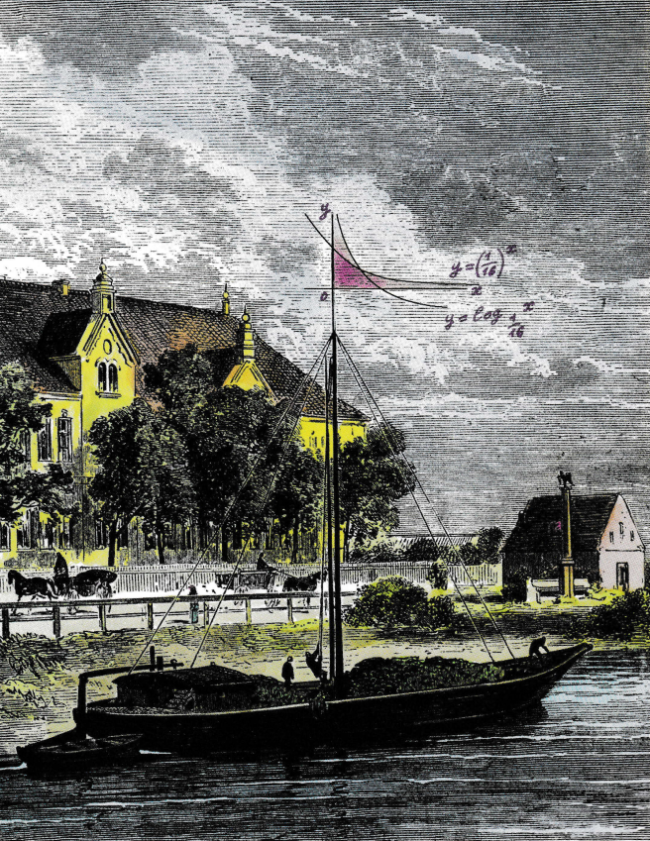
Mi mennyi?
"Megoldás"

Ez a megoldás hihetőnek tűnik, csakhogy . . .
. . . próbáljunk x helyére - az egyszerű számolás kedvéért - 1/2-et vagy 1/4-et írni!
Ez indokolta az idézőjelet! Az alábbi appletet vizsgálva kiderül, hogy a fenti rajz függvényeihez nem ezek a képletek tartoznak. Az is, hogy a két függvény monotonitása nem elegendő ahhoz, hogy csak egy közös pontjuk legyen.
Figyeljük meg, hogy ...
... a fenti appletben a csúszkával vezérelt paramétertől miként függ az f(x) és g(x) függvény metszéspontjainak a száma.
Mivel e két függvény egymás inverze, elegendő a (0,xA ) intervallumot elemeznünk, ahol xA az A az f(x), g(x) és a t(x)=x függvények közös pontja,ef(x) és eg(x) az exponenciális és logaritmus függvény A-beli érintője.
Ha a (0,xA) intervallumon eg(x) "alatta halad" ef -nek, akkor az A pont 0A környezetében g(x) is alatta halad efx) -nek, így f(x) -nek is. Ugyanakkor f(x) metszi az y tengelyt, g(x) nem, így e két függvénynek valahol egy A-tól különböző B pontban is metszeniük kell egymást, ahol xBA .
Mivel ef(x) és eg(x)-is tengelyesen tükrösek t(x)-re, ezért a fenti állapot igaz/hamis állapota akkor változik, ha ef(x)=eg(x) , vagyis, ha mindkettő merőleges t-re.
A mai technikai lehetőségek birtokában, a fenti applet mozgatásával könnyű erre az eredményre jutnunk, de az ezredforduló idején . . .
. . . e sorok írója ezt az - idézőjel nélküli - megoldást vehette kézbe, amelynek itt és most csak az első sorait mutatja be - nem kis büszkeséggel:

Németh József megoldása
Könnyű a dolgunk . . .
. . .ha már tudjuk, hogy mit kell kapnunk.
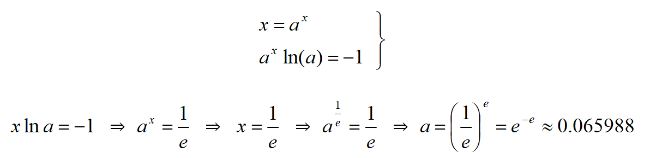
Minden füllentés (hamis bizonyítás) akkor hihető, ha közel áll az igazsághoz. Ez most is így van:
az a=e-e ≈ 0.065988 , miközben 1/16 = 0.0625. Például a=1/16 esetben az A ponthoz tartozó érintők szöge (ef(x),eg(x))∢≈0.58°
Nagy galádság ilyen feladattal fárasztani a gyanútlan ifjakat. Bár - mivel senki nem szereti, ha becsapják - , az ilyen problémák felkelthetik azok érdeklődését is, akiket egyébként egy-egy exponenciális függvény nem igazán tud lázba hozni.
Ha egy "jó" tanár arra szánja rá magát, hogy ilyesmivel traktálja az ugyancsak jó, érdeklődő tanítványait, helyes, ha van másik, hasonló "probléma" is a tarsolyában. Például az alábbi.
. . . .és most mi mennyi?
Hány megoldása van az x4=2x egyenletnek?
A probléma gyanútlan megoldója kézenfekvő módon lerajzolja az egyenlet két oldalának megfelelő függvényeket, erről leolvassa a "helyesnek vélt" választ: kettő.
Csakhogy. . . a gyanakvóbbaknak, óvatosabbaknak, alkalmasint felkészültebbeknek eszébe juthat, hogy bármely exponenciális függvény meredekebben tart a végtelenbe minden polinom függvénynél. Ez jelen esetben is így van: a nem is túl nagy x=16 érték ugyancsak kielégíti az egyenletet.
A fenti appletben az X tengelyen mozgatható M pont aktuális színe mutatja, hogy az adott xM abszcisszájú ponthoz melyik függvény ordinátája a nagyobb. Ezzel akár ki is lehet "tapogatni", hogy van-e az egyenletnek további gyöke.
A gyökök pontos, vagy közelítően jó megközelítése most nem tartozik a feladathoz, bár - jobb híján - az oroszlánfogás módszerével ez viszonylag könnyen megoldható. De erre most nincs szükségünk, A GeoGebrába beépített eljárás alkalmas arra, hogy a két függvény pozitív abszcisszájú metszéspontjait meghatározza, akkor is ha az egyik történetesen exponenciális függvény. Bár... ha az f(x) hatványkitevője egész, akkor az értelmezési tartománya kiterjed a negatív számokra is, és ha páros is az egyenletnek jól láthatóan van egy negatív gyöke is, bár ezt csak mi látjuk a GeoGebra nem. Egyelőre.
Ha "szabad a gazda", a ? jelű jelölőnégyzet megmutatja az egyenlet pozitív gyökeit. Nagyon érdeklődő felkészült olvasók - mint pl. N.J. - a ?? jelölőnégyzettel azt is megtudhatják, hogy hogyan kaptuk ezt az eredményt.
Az appletben egy-egy csúszkával adhatjuk meg mind az f(x)= xa polinomot, mind a g(x)=bx exponenciális függvényt meghatározó a ill. b paramétert.
A dinamikus geometriai programok - például a fenti - alkalmazásával felvetődhetnek olyan kérdések, amelyeket éppen ezek a - jelenesetben - 2≤a≤20 (egész) és 1.1≤b≤10 (0.1 pontosságú ) lépésenként beállítható értékek között változtatható paraméterek megválasztása ad a kezünkbe. Például:
- Van-e több olyan (a,b) számpár, amely ugyanazokat a pozitív gyököket állítja elő?
- Kísérletképpen becsüljük meg, hogy az eléggé szélsőséges a=20, b=1.1 esetben vajon mekkora lehet az egyenlet nagyobbik pozitív gyöke, és nagyságrendileg mekkora a metszéspont ordinátája?
- Milyen (a,b) számpárhoz tartozik egy (azaz két egybeeső) pozitív gyök, és mikor nincs pozitív gyöke az egyenletnek? Leírható-e egy függvénnyel az ilyen a és b paraméterek közötti kapcsolat?
Miért ennyi ....
Aki a fenti applet vizsgálata közben eljutott a ?? jelölőnégyzet bekapcsolásáig, olyan matematikai képletekkel találkozott, amelyekkel a GeoGebra megadta az xa=bx egyenlet pozitív megoldásait.
Mi ez a képlet? Mit kell(ene) tudni róla? Erre itt kapunk némi magyarázatot.
Ebből röviden az derül ki, hogy a könnyen ábrázolható y=x ex függvény inverze - az x=y ey függvény, amelyből az eddigi eszköztárunkkal nem fejezhető ki y. Ezért az inverz függvény megadására új jelölést kellett kitalálni. Többnyire az y=W(x) jelölést használja a matematikai szakirodalom, amelyre a GeoGebra az y=LambertW(x) jelölést alkalmazza. Mivel az y=x ex függvény megadása, lerajzolása nem okoz nehézséget a GeoGebra számára, így várhatóan az inverzét is le tudja rajzolni, tudja használni.
Mivel kaptuk?!
Könnyen belátható, hogy az s(x)=x ex függvénynek minimum helye van az x=-1 pontban ( amelynek az értéke -1/e ), így az s(x) függvény inverze a -1/e≤ x értelmezési tartományon vett f(x)=LambertW(x) függvény, Az x≤-1 esetben az s(x) inverze egy -1/e≤x<0 értelmezési tartományon megadott függvény, amelyet a GeoGebra g(x)=LambertW(x,-1) képlettel ír le.
Ha a GeoGebra ezt tudja, akkor tegyünk egy próbát. Vajon meg tudja-e oldani az egyenletünket általánosan, numerikus értékek használata nélkül. Erre a GeoGebra CAS - Computer Algebra System - alkalmazását hívjuk segítségül. Erről itt olvashatunk bővebben.
Oldjuk meg általánosan az x^a=b^x egyenletet!
Mit kaptunk?
Amint látjuk, a GeoGebra CAS alkalmazás készségesen megoldja a problémánkat.
Előbb óvatosan "arra gondol", hogy ha az a paraméterre vonatkozóan nincs információnk, előfordulhat, az ax kifejezés nem értelmezett a valós számok halmazán. Ezért "csak" azt a két gyököt adta meg eredményül, amely pozitív a és tetszőleges x esetben jöhet létre. Egyik esetben az előző rajzon kapott f(x)=LambertW(x) függvénybe, másik esetben a g(x)=LamvertW(x,-1) -be helyettesítve adta meg az a és b paraméterekből kapott kifejezés értékét.
Ha az a<0 eset miatti aggályát eloszlathatjuk azzal, hogy a helyett abs(a) -t írunk a parancssorba, egyből négy megoldást kapunk.
Miután megkaptuk általánosan is az egyenletünk gyökeit, anélkül hogy a programnak minden esetben újra kellene számolnia azokat, elegendő e képletekbe behelyettesíteni az a és b paraméter aktuális értékeit.
... de miért annyi, az ennyi?
Remélhetően sokunkat - így e sorok íróját is - zavarja, ha egy matematikai probléma megoldása - pontosabban: végeredménye - úgy bukkan elő, mint ahogy egy bűvész elővarázsolja a nyuszit az üres cilinderből, a nagyérdemű publikum legnagyobb ámulatára.
Milyen fogásokra - ügyeskedésre, bűvészkedésre - lehet szükségünk ahhoz, hogy ezeket a képleteket magunk is felírhassuk?
Mit kérdezne Pólya György? "Nem találkoztál már a feladattal? Esetleg a mostanitól kissé eltérő formában?"
Még nem, de találkozhattunk volna.
Meglepően sok YouTube videó akad, amely ezekre a fogásokra szeretne bennünket megtanítani:
5x +15=5^x , 10x=2^x , -x+5=2^x , 7x=5^(2 x) , 30-x=3^x , x^2= 2^x , x^5 = 9^x , x^5= 8^x
Ezeknek néha kellemes, akár fejben is kitalálható gyökei (is) lehetnek . Mindössze egy előadó kezdi a megoldást azzal, hogy lerajzolja a kiválasztott egyenlet két oldalának megfelelő függvényt. (De azon mód le is törli.) Körültekintő diszkusszióról egyáltalán nem esik szó. Ezek a megoldások lényegében ugyanazt a "fogást " sulykolják. (Ugyancsak Pólya szerint: "A módszer olyan fogás, amit kétszer alkalmazunk." )
Ha egy egyenlet exponenciális függvényt, és valamilyen polinomot is tartalmaz, igyekezzünk azt p(x)ep(x)=k alakra hozni, ahol k az egyenlet paramétereiből (konstansaiból) álló kifejezés, és p(x) -ből elemi eszközökkel kifejezhető x. Ugyanis mivel LambertW(p(x)ep(x))=p(x), az egyenlet átírható p(x)=LambertW(k) alakba, amiből már kibonthatjuk x-et.
Ez valóban igényel némi ügyeskedést, feladatmegoldói rutint. Ezen túlmenően szem előtt kell tartanunk, hogy mindkét LambertW() függvény értelmezési tartománya és értékkészlete is korlátozott.
Az ördög mindig a részletekben van, ...
...így most is. Lássuk tehát a részelteket.
Oldjuk meg "kézzel", számítógép alkalmazása nélkül, de a LambertW() függvény(ek) ismeretében -
az |x|a=bx egyenletet, ahol 0 < a és 1 < b !
- Az |x| feltételt oldjuk fel azzal, hogy külön foglalkozunk előbb a 0< x esettel! Ekkor: xa=bx
- Vegyük az egyenlet mindkét oldalának az e alapú logaritmusát: a ln(x) = x ln(b)
- Rendezzük az egyenletet x-re: ln(x)/x=ln(b)/a
- Mivel ln(x)= -ln(1/x) , így ln(x)/x=-ln(1/x) eln(1/x) így: ln(1/x) e ln(1/x)=-ln(b)/a
- Vegyük mindkét oldal mindkét LambertW() függvényét és használjuk ki a LambertW(p(x) ep(x))=p(x) összefüggést: ln(1/x)=LambertW(-ln(b)/a-1) ln(1/x)=LambertW(-ln(b)/a)
- Tekintsük az egyenlet mindkét oldalát egy e alapú hatvány kitevőjének, majd vegyük minkét oldal reciprokát: x=e-LambertW(-ln(b)/a,-1) x=e-LambertW(-ln(b)/a) Ezzel megkaptuk az egyenlet pozitív gyökeit.
- Visszatérve az x<0 esetre, az 1. lépésben |x| helyére -x et kell írnunk. Mivel most -x pozitív, így létezik a logaritmusa: a ln(-x)=(-x) ln(b).
- Ebből: ln(-x) (-x)-1=ln(b)/a.
- a 3. lépésben, mivel ln(-x)= -ln(-1/x): (-ln(-1/x)) e-ln(-1/x)=ln(b)/a, így az egyenlet másik két gyöke: x=-e-LambertW(ln(b)/a,-1) Egy komplex szám. (??) x=-e-LambertW(ln(b)/a) Az eredeti egyenlet negatív gyöke.
Vegyük észre, hogy ...
... az a és b paraméterek 0.01 pontosságúra állíthatók, sőt konkrét értékeket tudunk írni a parancs sorba.
Pl: a=3.14, a=Pi , vagy akár a=e ln(b). (Ha kísérletezés közben esetleg elveszik egy csúszka, a jobb felső sarokban lévő ↷ jellel állítsuk vissza a kezdő állapotot.)
A bal oldali rajzlapon rendre megjeleníthető, hogy a - többszörösen összetett - függvényekkel kapott gyökök miként állnak elő az a és b paraméterből.
Az már talán nem is meglepő, hogy ha az egyenlet két pozitív gyöke egybeesik, akkor ez a gyök éppen e .
