Yamuk Ders Notları
Tanım: Karşılıklı kenar çiftlerinden en az bir tanesi birbirine paralel olan dörtgenlere yamuk denir.
Birbirine paralel olan kenarlar taban, diğerleri ise yan kenar şeklinde isimlendirilir.
Elbette dörtgen ailesinin bir üyesi olduğundan, dörtgene ait tüm özellikler yamuk için de geçerlidir.
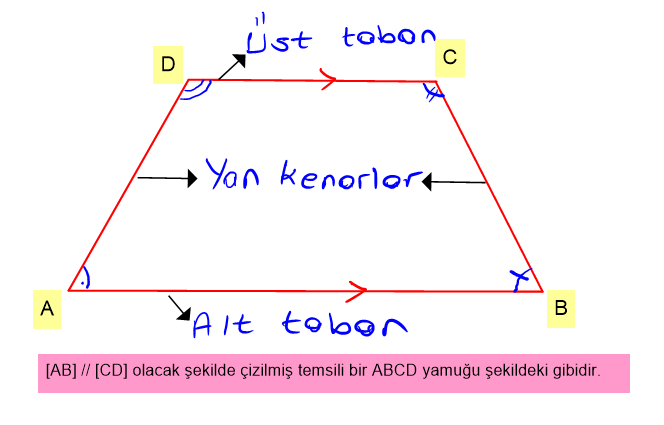
Ortak yan kenarı paylaşan alt ve üst tabandaki komşu açıların ölçüleri toplamı 'ye eşittir.
Yukarıdaki şekilde:
ve
dir. Aşağıda; hem bu eşitlikleri gösteren, hem de köşelerin hareket ettirilmesiyle ortaya çıkan sonuçların gözlemlenebileceği bir etkinlik bulunmaktadır.
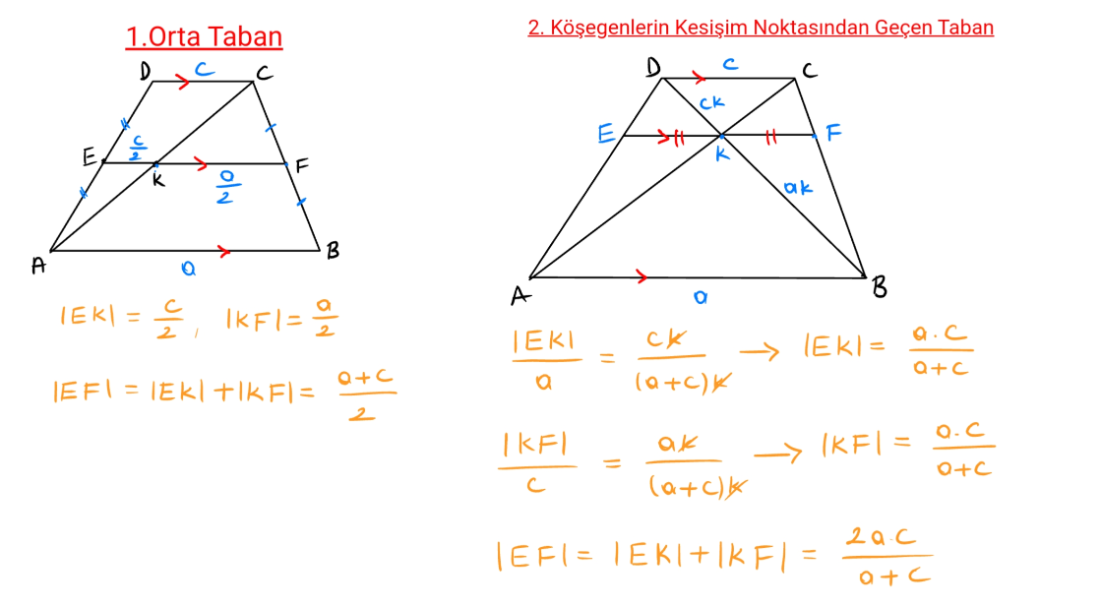
Yamuğun yan kenarlarının orta noktalarını birleştiren doğru parçasına orta taban denir.
Orta tabanın uzunluğu; taban uzunluklarının aritmetik ortalamasına eşittir.
Yamuğun köşegenlerinin kesişim noktasından geçen tabanlara paralel doğru parçası; taban uzunluklarının harmonik ortalamasına eşittir.
Aritmetik ve harmonik ortalamaya benzer biçimde; geometrik ve karesel ortalama da uçları yan kenarlar üzerinde olan tabanlara paralel doğru parçaları vasıtasıyla gösterilebilir. Önce bu ortalamaların hesaplama bağıntılarını sırasıyla yazalım. olmak üzere ve pozitif tam sayıları verilsin, bu iki sayı kullanılarak ortalamalar: 1. Aritmatik Ortalama: 2. Geometrik Ortalama: 3. Harmonik Ortalama: 4. Karesel Ortalama: şeklinde hesaplanır. Genel olarak ve ile birlikte yukarıdaki dört ortalama arasında; eşitsizlikleri geçerlidir. Aşağıda; bu eşitsizliklerin bir yamuğu üzerinde gözlemlenebileceği dinamik bir etkinlik düzeneği verilmiştir.
Her bir ortalama için çizilen tabanlara paralel doğru parçası, geometrik açıdan anlamlı bir karşılığa sahiptir.
1. Harmonik Ortalama; yamuğun köşegenlerin kesişim noktasından doğru parçasının,
2. Geometrik Ortalama; Yamuğu birbirine benzer iki küçük yamuğa bölen doğru parçasının,
3. Aritmetik Ortalama; Yamuğun orta tabanı olan doğru parçasının,
4. Karesel Ortalama; Yamuğun alanını iki eşit parçaya bölen doğru parçasının,
uzunuluğuna eşittir.
Ortalamalarla alakalı daha detaylı bilgiye; Hüseyin Demir'in 1991 yılı Matematik Dünyası dergisi 1'inci sayısında yayımlanan yazısından ulaşabilirsiniz. (Sayfa 17-21)