S6G1 点列的回归曲线
引入介绍
给定一串点列,如何找到合适的拟合曲线呢?在 Geogebra 中已经内建统计数值分析模型,方便我们直接获取数据的一维与二维的统计资料分析。在二维的数据分析中,还可切换 [线性/指数/成长曲线/多项式/逻辑拟合] 等回归模型。在这次案例,我以我【学用数学】公众号的关注人数来作一个初步的回归分析。
背景说明
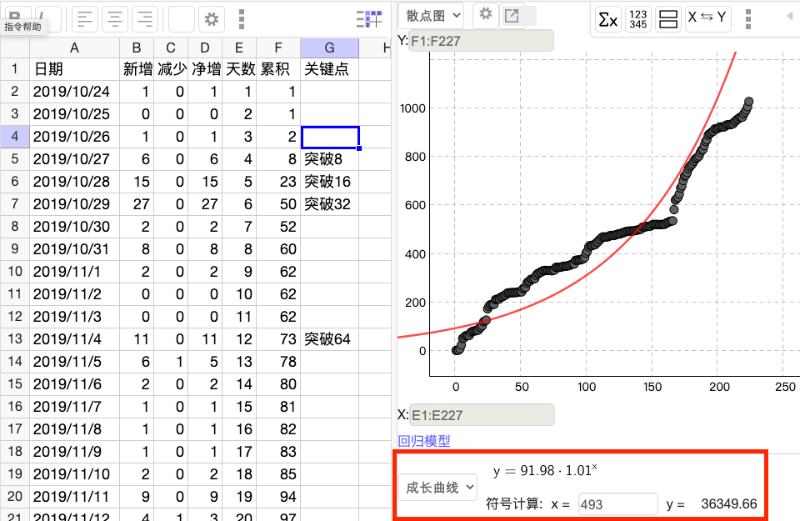
这次分析的资料是 [学用数学] 从 2019/10/24 到 2020/6/3 公众号的订阅人数数据。在用线型回归模型时,得到回归直线为 y=4 x + 21 。表示这段期间在以每日 4 人的数量在增加。
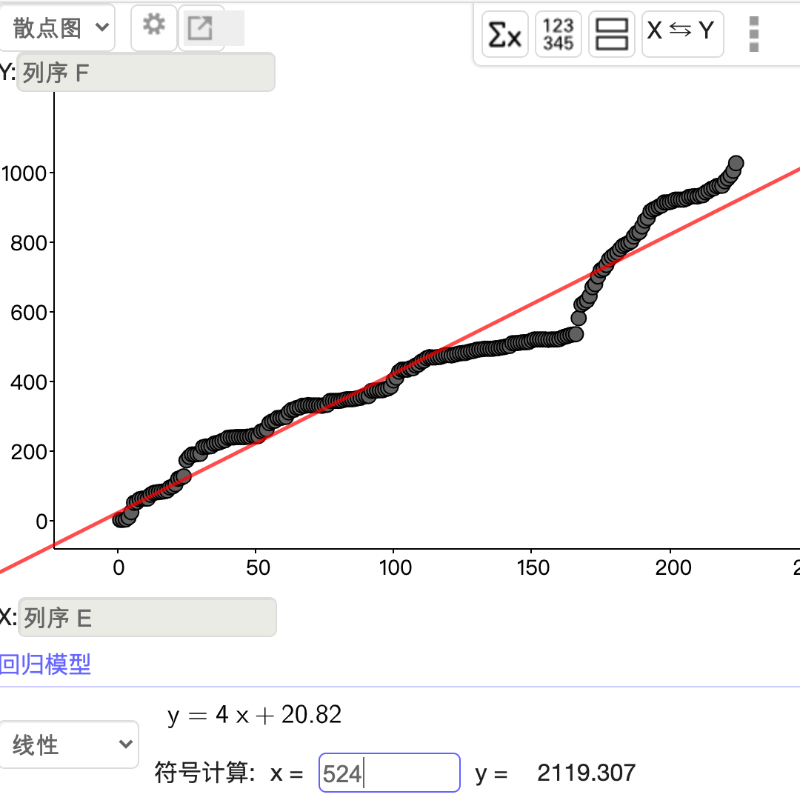
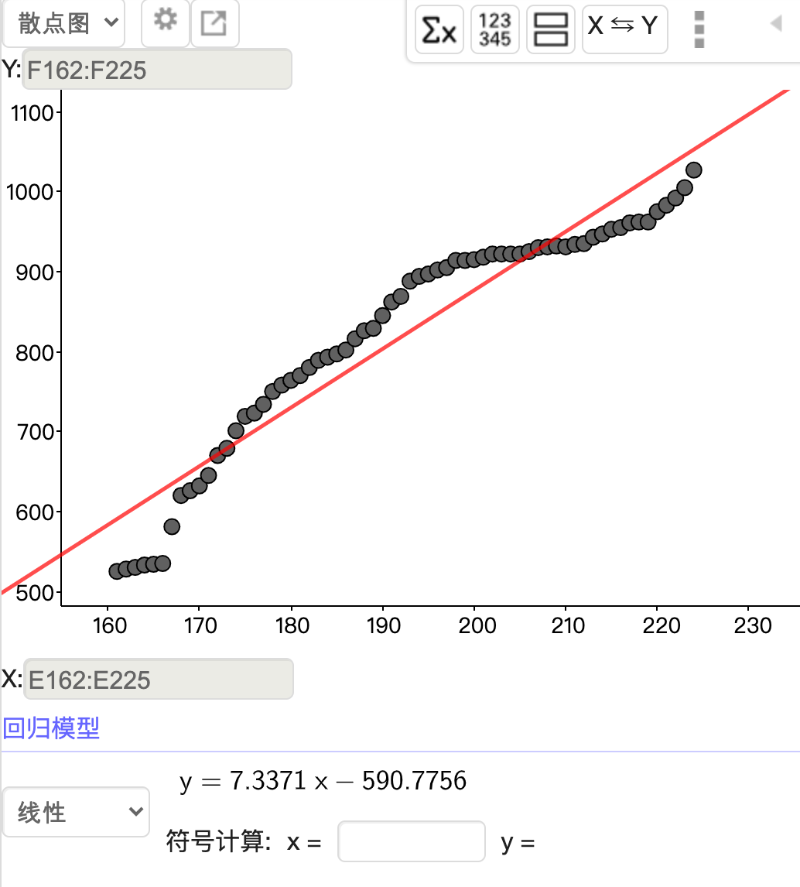
但这图形后半段的增幅较大,若对 2020/4/1 到 2020/5/3 作回归分析可得 y = 7.3x - 590 。在这一个月是以每天7.3 人的增量在增长。而在在 2019/10/24~2020/3/31 这60天的平均日增约是 3 人。
若用【成长曲线】来作回归可得 y = 92*1.012^x 。在回归选项中还有个【指数曲线】也是会得到相同的函数,只不过在其解析式是用 e 为底来表示,在此例写为 y = 92xe^(0.01x) 。
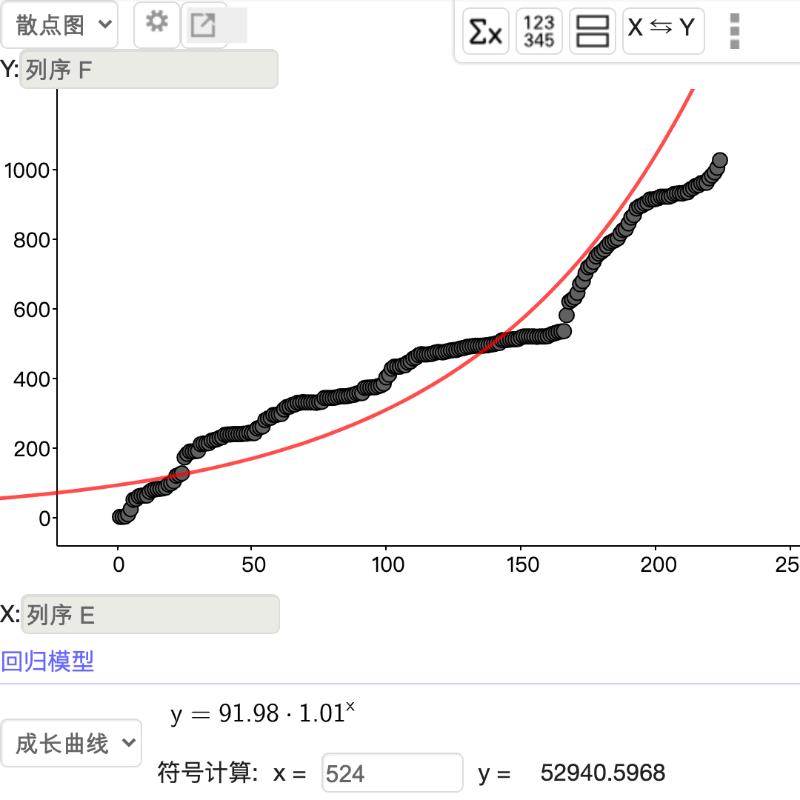
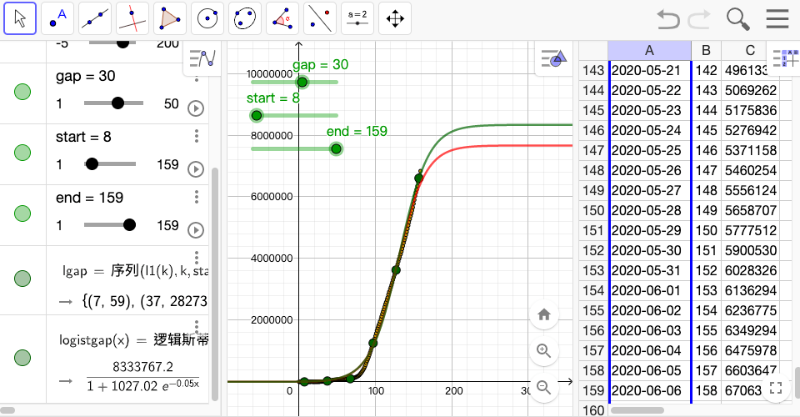
然而对于人口规模模型,一般都无法持续等比增长,比较合理的增长都是用 logistic 回归(逻辑斯蒂曲线拟合)。在这模型会有个数量的最大上限,以目前这个数据得到的数值为 2975。
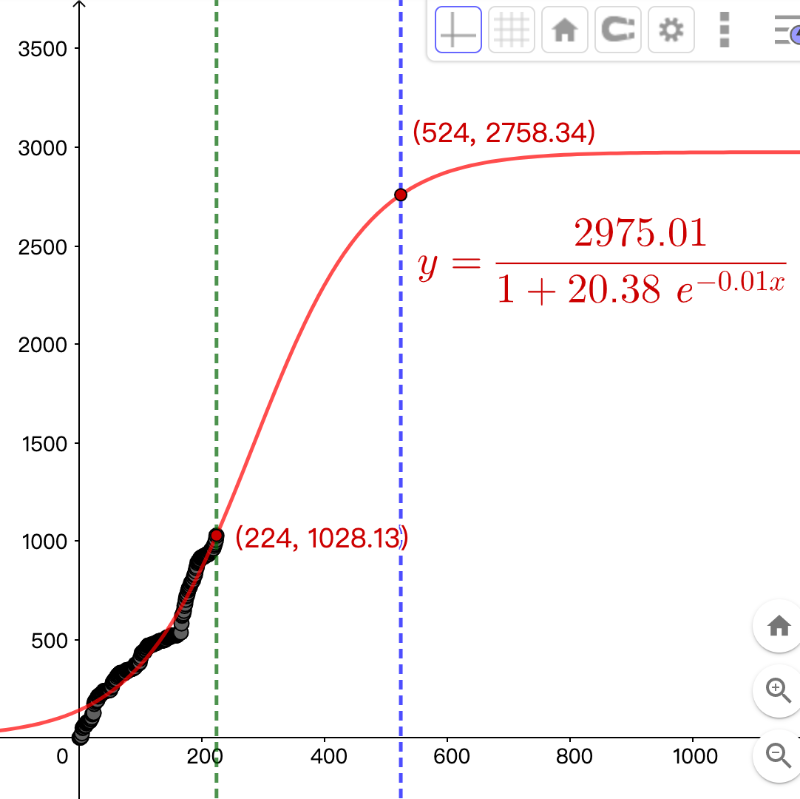
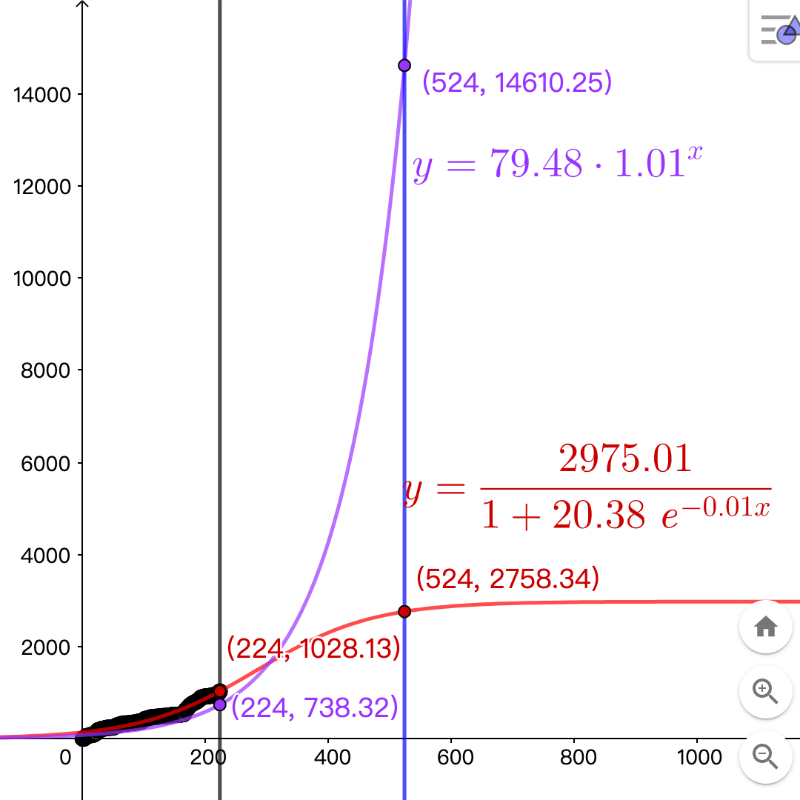
而我期待在 40岁生日前关注人数达到 14610 人,利用这个预期数据找出如下几类拟合曲线。以指数拟合,每日 1.01倍再增长,则其函数为 y=79.5*1.01^x 。若用 Logistic 拟合,设定通过 (224,1024), (524,14610), (730,16384) 这三点,则得到函数为 y = 16472/(1+534*exp(-0.02x))。用三次多项式拟合现有的数据得到的为蓝色曲线,y=0.000169x^3-0.05x^2+7.13x 。
学习指引
这次主要是认识 Geogbra 的曲线拟合功能。这次定位为 Lv 4 的难度,在学习这个课程时。若是 Lv1~2 的新手,可只完成【任务一】的部分,同时建议复习基础教程中的 《S411L3 表格区与递回关系》的基础教学视频。在【任务二】将利用序列对原资料作些重新取样与调整。在【任务三】会在了解、[多项式拟合]与[逻辑斯蒂拟合]。在本次任务,你将学会以下目标:
数学思维
- 理解线性拟合与直线回归方程
- 理解曲线拟合的使用
- 利用表格区的[双变数回归分析]
- [多项式拟合]、[逻辑斯蒂曲线拟合]
学习指引
这次主要是认识 Geogbra 的曲线拟合功能。这次定位为 Lv 4 的难度,在学习这个课程时。若是 Lv1~2 的新手,可只完成【任务一】的部分,同时建议复习基础教程中的 《S411L3 表格区与递回关系》的基础教学视频。在【任务二】将利用序列对原资料作些重新取样与调整。在【任务三】会在了解、[多项式拟合]与[逻辑斯蒂拟合]。在本次任务,你将学会以下目标:
数学思维
- 理解线性拟合与直线回归方程
- 理解曲线拟合的使用
- 利用表格区的[双变数回归分析]
- [多项式拟合]、[逻辑斯蒂曲线拟合]
练习任务
在完成这次的三个任务后,你可在用 Covid-19 的资料来作个相关的练习。