Układ kartezjański
Kartezjański układ współrzędnych prostokątnych określimy następująco:
Przez dowolny punkt przestrzeni prowadzimy trzy proste wzajemnie do siebie prostopadłe zwane osiami współrzędnych: , i . Współrzędnymi punktu są miary rzutów wektora na poszczególne osie układu. Znaki współrzędnych zależą od tego, czy wektory mają zwroty zgodne z osiami współrzędnych czy przeciwne. Punkt nazywamy początkiem układu współrzędnych. Płaszczyzny: , , dzielą układ na oktanty (ósemki) przestrzeni. Współrzędne punktu nazywamy odpowiednio: odciętą, rzędną, kotą.
Jeśli pominiemy warunek prostopadłości prostych, to tak utworzony układ nazywamy układem współrzędnych ukośnokątnych.
Ćwiczenie 1.
Poruszając punktem , ustaw jego współrzędne: .
Aby ustawić współrzędne wybranego punktu należy najechać na niego kursorem i wybrać jedną z dwóch możliwości jego przemieszczania:
- pionowo (po prostej równoległej do osi )
- poziomo (w płaszczyźnie równoległej do płaszczyzny )
Uwaga.
Wyróżniamy dwa rodzaje kartezjańskich układów współrzędnych prostokątnych: prawoskrętny i lewoskrętny.
W GeoGebrze standardowo otrzymujemy wykresy w układzie prawoskrętnym. Aby uzyskać układ lewoskrętny trzeba zmienić etykiety osi oraz nazwy współrzędnych.
Układ prawoskrętny
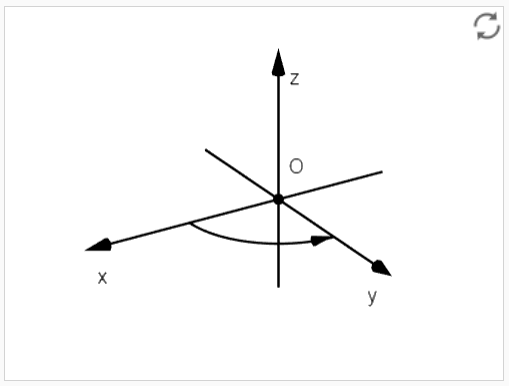
Układ lewoskrętny
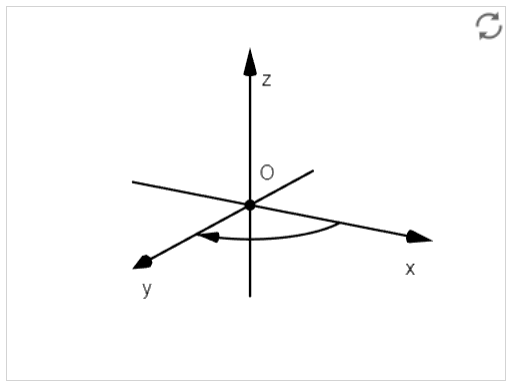
Ćwiczenie 2.
Przesuń punkt , tak by znalazł się w pierwszym oktancie układu (tzn. by jego wszystkie współrzędne były dodatnie).