Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Inkreis eines Dreiecks

Autor:JHäring

Aufgabenstellung

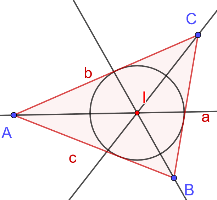
Der Inkreis eines Dreiecks ist der Kreis, der alle Seiten von innen genau einmal berührt. Konstruiere mithilfe des GeoGebra-Applets (siehe unten) ein Dreieck mit den Eckpunkten       A(-5|-1), B(4|-2), C(2|3) sowie den Inkreis dieses Dreiecks. Die folgende Konstruktionsanleitung hilft dir dabei.
Inkreis eines Dreiecks
Inkreis eines Dreiecks

Konstruktionsanleitung

1Toolbar ImageKonstruiere das Dreieck ABC: Klicke auf das Werkzeug Vieleck und lege die Eckpunkte des Dreiecks in der Aufgabenstellung fest.2Toolbar ImageZeige die Beschriftung der Punkte A,B,C und der Seiten a,b,c an: Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um die Beschriftung anzeigen zu lassen.3Toolbar ImageErzeuge die drei Winkelhalbierenden des Dreiecks: Klicke auf das Werkzeug Winkelhalbierende und anschließend auf drei Punkte. Die Winkelhalbierende verläuft durch den als zweites ausgewählten Punkt.4Toolbar ImageStelle die Winkelhalbierende gestrichelt dar: Klicke auf das Werkzeug Bewege und anschließend mit links auf das entsprechende Objekt. Klicke auf die Gestaltungsleiste rechts oben und ändere die Darstellung des Objekts.5 Toolbar ImageBeschrifte die Winkelhalbierenden mit wa, wb, wc : Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um es umzubenennen. Um wa zu schreiben, stelle einen Unterstrich voran, etwa w_a. 6Toolbar ImageErzeuge den Inkreismittelpunkt des Dreiecks: Klicke auf das Werkzeug Schnittpunkt und anschließend auf zwei der soeben konstruierten Winkelhalbierenden.7Toolbar ImageKonstruiere die drei Senkrechten zu den Seiten des Dreiecks durch den Inkreismittelpunkt: Klicke auf das Werkzeug Senkrechte Gerade. Klicke auf eine der Seiten des Dreiecks und anschließend auf den Inkreismittelpunkt.8Toolbar ImageKonstruiere die drei Schnittpunkte zwischen den Senkrechten und den Seiten des Dreiecks: Klicke auf das Werkzeug Schnittpunkt. Klicke auf eine Senkrechte und anschließend auf eine Seite des Dreiecks. 9Toolbar ImageBlende die drei Senkrechten aus: Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt, um "Objekt anzeigen" zu deaktivieren. 10Toolbar ImageKonstruiere den Inkreis des Dreiecks: Klicke auf das Werkzeug Kreis mit Mittelpunkt durch Punkt und anschließend auf den erzeugten Inkreismittelpunkt. Klicke danach auf einen der drei soeben konstruierten Schnittpunkte.

Verständnisaufgaben bzw. -fragen

Bewege die Punkte A,B und C im GeoGebra-Applet um die folgenden Aufgaben zu lösen bzw. Fragen zu beantworten.

Entscheide, ob die folgende Aussage wahr oder falsch ist: Jedes Dreieck besitzt genau einen Inkreis.

Wähle alle richtigen Antworten aus
  • A
  • B
Antwort überprüfen (3)

Entscheide, ob die folgende Aussage wahr oder falsch ist: Die drei Winkelhalbierenden des Dreiecks schneiden sich immer in genau einem Punkt.

Wähle alle richtigen Antworten aus
  • A
  • B
Antwort überprüfen (3)

Für welche Koordinaten der Punkte A,B und C liegt der Umkreismittelpunkt genau im Koordinatenursprung (0|0)?

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

Entscheide, ob die folgende Aussage wahr oder falsch ist: Der Inkreismittelpunkt liegt immer innerhalb des Dreiecks

Wähle alle richtigen Antworten aus
  • A
  • B
Antwort überprüfen (3)

Welches Problem entsteht, wenn die Punkte A,B und C die Koordinaten A(-5|-2), B(-2|-1) und C(1|0) haben? Formuliere deine Beobachtung in einem Freitext.

Antwort überprüfen

Entscheide, ob die folgende Aussage wahr oder falsch ist: Wenn die drei Punkte A,B und C "fast" auf einer Geraden liegen, ist der Inkreis groß.

Wähle alle richtigen Antworten aus
  • A
  • B
Antwort überprüfen (3)

Entscheide, ob die folgende Aussage wahr oder falsch ist: Wenn das Dreieck gleichseitig ist, ist der Inkreis groß.

Wähle alle richtigen Antworten aus
  • A
  • B
Antwort überprüfen (3)

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen