Función de densidad o función de probabilidad
Recordamos conceptos del tema anterior:
- Variable aleatoria , función que asocia a cada elemento del espacio muestral un número real
- Variable aleatoria discreta; si toma un número finito de valores, en general números enteros
- Variable aleatoria continua; si toma infinitos números reales de un intervalo.
Pregunta 1.-
Selecciona cuáles de estas variables aleatorias son variables de probabilidad continua:
En el caso de las V.A discretas definíamos la función de probabilidad asociando a cada posible resultado de la variable su probabilidad, tablas de probabilidad , y a partir de las tablas obteníamos la y la .
En el caso de las V.A continuas, la probabilidad de que tome un determinado valor en concreto es 0 (tenemos infinitos valores) . Calcularemos entonces en este tipo de distribuciones, la probabilidad de que la V.A sea mayor o menor que un número, o este comprendida en un intervalo.
Para ellos, modelizando distribuciones estadísticas, llegamos a definir una curva llamada función de densidad o función de probabilidad.
Esta función de densidad, tiene dos propiedades importantes:
- El área encerrada bajo la curva es la unidad.
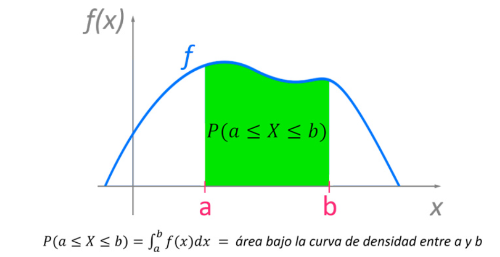
El símbolo es la integral de la función que no veremos hasta 2º de bachillerato.
En este curso , nos centraremos dentro de las distribuciones de variable continua en la DISTRIBUCIÓN DE PROBABILIDAD NORMAL. Para el calculo de las probabilidades de esta nosotros no haremos integrales, ya las han hecho por nosotros, utilizaremos la TABLA DE PROBABILIDAD DE LA NORMAL que recoge todos estos cálculos.
Pregunta 2.-
¿Calcularemos integrales en este curso?