Berechnung des Vektorprodukts
Definition des Vektorprodukts
Unter dem Vektorprodukt (sprich: a kreuz b) zweier Vektoren und versteht man den Vektor mit folgenden Eigenschaften:
- steht normal sowohl zu als auch zu .
- gibt den Flächeninhalt des von den Vektoren und aufgespannten Parallelogramms an.
- Die Vektoren , und bilden in dieser Reihenfolge ein rechtshändiges System.
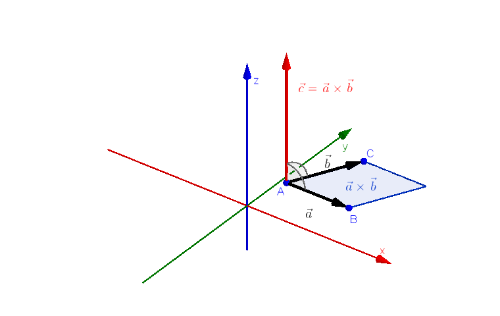
Zur Berechnung des Vektorprodukts
Aus den in der Definition formulierten Eigenschaften des Vektorprodukts (Kreuzprodukt) kann eine Formel zur Berechnung angeleitet werden.
Sei , und
Aus Punkt (1) der Definition folgt
Aus Punkt (2) der Definition folgt mit der Flächenformel in Vektorform
Aus diesen drei Gleichungen kann das Vektorprodukt berechnet werden, indem das Gleichungssystem nach xc, yc und zc gelöst wird.
Aus den beiden Lösungen des Gleichungssystems ergibt sich aufgrund des Rechtssystems - siehe Definition Punkt (3) - folgende Formel für das
Vektorprodukt (Kreuprodukt) zweier Vektoren und im