Ilyen állat nincs!
- mondta az egyszeri ember, amikor életében először meglátott egy zsiráfot az állatkertben.
Ez volt a kedvenc mondása egykori tanáromnak és mentoromnak Csákány Bélának, amikor hihetetlennek tűnő dologgal találkozott.
Ezt mondta akkor is, amikor kezébe vette a - jóval később - Szilassi-poliédernek nevezett geometriai konstrukciót.. Most én kerültem hasonló helyzetbe. Ezt a messze nem szokványos történetet szeretném megosztani olvasóimmal.
Can I Solve This Unsolved Math Problem?

2025. január 20-án
bukkantam egy YouTube videóra, majd egy ezzel kapcsolatos weblapra:
https://github.com/HackerPoet/NeighborlyPolyhedra
Mindez röviden arról szól, hogy a szerző arra tesz kísérletet, hogy a tetraéderen és a Szilassi-poliéderen* kívül keressen olyan közönséges poliédert, amelynek bármely két lapja szomszédos.
* Nem kis szerénytelenséggel, a rövidség, egyértelműség kedvéért én is így hivatkozom erre a konstrukcióra.
Az előzmények
Idézzünk fel néhány - reményeink szerint könnyen követhető - gráfeméleti, topológiai fogalmat.
Teljes gráfnak nevezzük azt a véges gráfot, amelynek bármely két csúcsát pontosan egy él köti össze.
Felületre rajzolható (feszíthető) az a gráf, amelynek minden éle (a csúcsait összekötő folytonos vonal) illeszkedik a felületre, úgy, hogy az élek nem metszik egymást.
Belátható, hogy az n csúcsú teljes gráf csak akkor rajzolható a síkra - ezzel egyenértékű módon a gömbre - , ha n≤4 . Így p.l az 5 csúcsú teljes gráf már nem rajzolható a síkba.
Egyszerűen megfogalmazható, de körültekintő bizonyítást igényel Euler poliéder-tétele, miszerint minden síkba rajzolt véges gráfra érvényes az C+L-E=2 összefüggés, ahol C a gráf csúcsainak E az éleinek L a lapjainak (tartományainak) a száma, amelyekre a gráf élei felbontják a síkot.
Ennek a tételnek az általánosítása az un. Euler - karakterisztika fogalma és az erre vonatkozó tétel. Eszerint ha egy irányítható felületre rajzolunk egy C csúcsú, E élű és L tartományú egyszerű, véges gráfot akkor
C+L-E=2-2k , ahol k a felület Euler karakterisztikája, amely egy adott felületre jellemző szám, amely független attól, hogy éppen hány lapja, csúcsa és éle van az adott felületre rajzolt gráfnak.
Egy k Euler karakterisztikájú felületet -topológiai azempontból vizsgált objektumként például úgy állíthatunk elő, hogy a gömbön vágunk k darab kör alakú lyukat, és ezeket beragasztjuk egy-egy "fogantyúval",amelynek a határvonala ugyancsak kör. Ennek a tételnek az igazolása messze túlmutat a lehetőségeinken, alkalmazása viszont nem.

Felületre rajzolt teljes gráfok
Vessük fel azt a kérdést, hogy melyek azok a felületek, amelyekre rajzolható teljes gráf.
Legyen egy ilyen gráfnak C csúcsa, E éle és L tartománya! Egy ilyen tartomány (topológiai értelemben) csak háromszög lehet, hiszen például egy négyszögtartomány átlói metszenék egymást. minden él pontosan két csúcsot köt össze és két tartományt választ el. Ebből : C (C-1)=2E és 3L=2E Így
C+C((C-1)/3 - C(C-1)/2 = 2-2k . Ebben az egyenletben C-nek és k-nak egész számnak kell lennie.
Ez különböző k érték esetén egy-egy C-re nézve másodfokú egyenletet jelent , amiből
- Ha k=0 , akkor C=4, L=4 , L=6 - ez a tetraéder gráfja.
- Ha k=1, akkor C=7, L=14, E=21 ez a tóruszra rajzolt teljes gráf. 1949 óta tudjuk, hogy ez a gráf poliéderként is realizálható, ez a Császár poliéder; 1890 óta tudjuk, hogy ennek a gráfnak a duális gráfja, az a tóruszra feszíthető gráf amelynek L=7 hatszögből álló tartománya , C= 14 olyan csúcsa van, amely mindegyikéből 3 él indul ki, így az éleinek a száma 21. 1977 óta tudjuk azt is, hogy ez a gráf ugyancsak realizálható közönséges poliéderként, ez a Szilassi-poliéder
- Ha 1<k<6 akkor a fenti egyenletből C-re nem kapunk egész értéket, azaz nincs 2, 3, 4 vagy 5 csúcsú zárt, irányított felületre rajzolható teljes gráf.
- Ha k=6 , akkor C=12, L=44 , E=66. Tehát a hat lyukú tóruszra kifeszíthető a 12 csúcsú teljes gráf, vagy ennek a duálisa, amelynek az L=12 lapja 11 oldalú sokszög , C=44 csúcsának mindegyikébe 3 él fut be és E= 66 éle van. De vajon vannak-e ilyen topológiai tulajdonságú közönséges poliéderek?
De mit is keressünk?
Lényegében olyan közönséges poliédereket, amelyek bármely két lapja szomszédos.
Tekintsünk most el sokszög és a poliéder fogalom teljes kiépítésétől, azonban tisztázzuk, mit tekinthetünk "közönséges" poliédernek.
Közönséges poliédernek nevezzük azokat a poliédereket, amelyeket
- véges sok egyszerű sokszöglap határol, vagyis a sokszög határvonala nem lehet önátmetsző;
- továbbá bármely két lapjának legfeljebb két közös csúcsa van, és ha pontosan két csúcsuk közös, akkor az ezekhez tartozó szakasz a két - szomszédosnak nevezett - lap közös éle;
- a poliéder lapjainak további közös pontjai nincsenek. Sem a sokszög határvonalán, sem a sokszög belső pontjai között. Ez a feltétel biztosítja, hogy maga a poliéderfelület ne legyen önátmetsző. Úgy is fogalmazhatjuk: ne ütközzenek a lapok egymással.
A meglepetés
Ezeket az előzményeket végig követve képet kaphatunk arról, hogy az iménti kérdés mennyire bonyolult.
A fenti Yqutube videó lényegében az ilyen 12 egymással páronként szomszédos lapból álló poliéderek kereséséről szól.
A szerző azzal próbálta egyszerűsíteni a kérdést, hogy olyan poliédert keresett, amelynek három, egymásra páronként merőleges szimmetriasíkja van. Így elegendő volt -lett volna - azt a három sokszöget megkeresni, amelyekből a három szimmetriasíkra vonatkozó tükrözéssel előáll a keresett 12 lapú poliéder.
A kérdés még ilyen egyszerűsítés mellett is óriási, szerteágazó. Ugyanis addig, a míg a k=1 Euler-karakterisztikához csak egy kombinatorikus elrendezés tartozhat, addig a k=6-hoz 59. Vagyis 59 különböző elrendezésű - egymással nem izomorf - teljes gráf feszíthető rá egy hatlyukú tóruszra. Ezek mindegyikét meg kell(ene) vizsgálni.
Ez meg is történt. Ha csak egy önátmetsző lap maradt volna, a szimmetria kapcsolatok miatt ez rögtön 4 önátmetsző lapot eredményezett volna a z egész konstrukción. Ugyanígy ha két lap "ütközött" akkor ez is négy lap-pár ütközését jelentette. Már az is szép eredménynek tekinthető, hogy sikerült ütközés mentes, de legalább 8 önátmetszést tartalmazó, vagy önátmetszés mentes, de legalább nyolc ütközést tartalmazó változatokat találni. Erről szó a videó.
Végül a szerző megpróbálkozott azzal, hogy csak egyetlen tengelyes szimmetriát szabott ki kezdő feltételként, így sikerült találnia egy olyan poliédert, amelynek lényegében egy (a tengelyes szimmetria miatt kettő) önátmetsző lapja van, és a lapok között nincs ütközés.
Ezt az eredményt itt közölte:
https://github.com/HackerPoet/NeighborlyPolyhedra/issues/3
Ennek a felhasználásával készült - az itt részletezett módon - az alábbi GeoGebra applet.
Az N-dodekéder
Az applet egy olyan tizenkét lapú poliédert - mondhatnánk: dodekaédert - mutat be, amelyben bármely két lapnak pontosan egy közös éle van.
Házi használatra nevezzük az így kapott konstrukciót N-dodekaédernek. Az N betű jelenthetné a Nem ismert, Nehéz , Neighbouring (szomszédos) szavakra is.
Az alakzat tengelyesen szimmetrikus, ezért az egymással egybevágó lapokat azonos színnel jelöltük.
A lapok láthatósága egyenként ki-be kapcsolható. Javasoljuk olvasóinknak, hogy a lapokat az önátmetszést vizsgálva egyenként, az ütközésmentességet ellenőrizve néhányat vegyenek szemügyre egyszerre.
Vegyük észre, hogy ...
- az 5. és 6. lap önátmetsző;
- ha megjelenítjük a poliéder csúcsait, lehetőségünk nyílik szemügyre venni a két nem kívánt önátmetsző pontot;
- bár a 4. és 5. lap közös éle másutt van, ezeknek van két olyan élük, amelyek metszik egymást. Ugyanez a 3. és 6. lapnál is így van. Ez is az egyetlen hiba következménye.
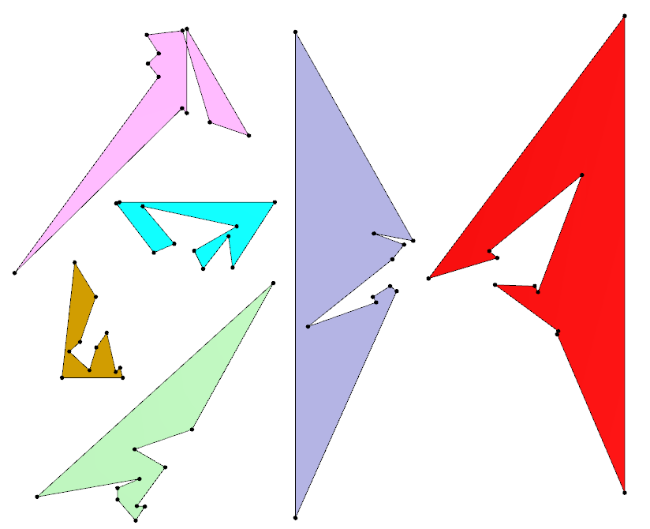
Az N-dodekaéder hat különböző lapja