Algorithm for finding the expected location of Local maxima or minima of stationary points of a function of two variables in the coordinate descent-ascent method
Algorithm for finding the expected location of Local maxima or minima of stationary points of a function of two variables in the coordinate descent-ascent method
I used
- contour map or heat map to approximate the location of stationary points for a function of two variables,
- GeoGebra Maximize/Minimize commands using the coordinate ascent-descent method, applying the coordinate sliders X and Y to numerically find the desired maxima/minima.
At each iteration step (initially variation by X, then by Y) we have a new point E:=(X,Y) and then the variation interval around the new point decreases: x(E)-p <X<x(E)+p and correspondingly y(E)-p<Y<y(E)+p. p is the radius of the circle described around point E. po is the initial radius, then it decreases according to the law p:=p*q. I have q=0.75.
Problems.
First. The accuracy of calculations in the Geogebra algebra section is limited. At the final stage, the result is refined using the CAS section, where the accuracy of calculations is much greater.
Second. The Maximize/Minimize commands do not necessarily find the "most" local extreme values. Therefore, at each step, all previous ones are sorted and the most optimal step is selected.
| | X:=cx; Y:=cy, If[SIndex==1,Execute[{"SetValue[cx,Maximize[f_{cxcy},cx]]","SetValue[cy,Maximize[f_{cxcy},cy]]" } ]] If[SIndex==2,Execute[{"SetValue[cx,Minimize[f_{cxcy},cx]]","SetValue[cy,Minimize[f_{cxcy},cy]]" } ] ] |
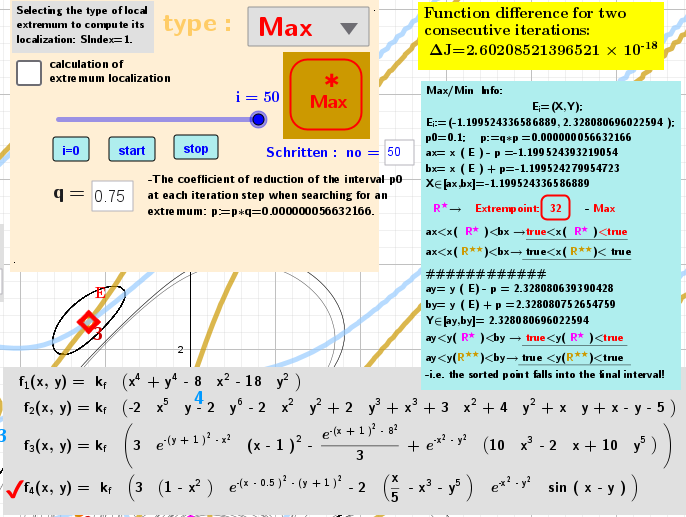
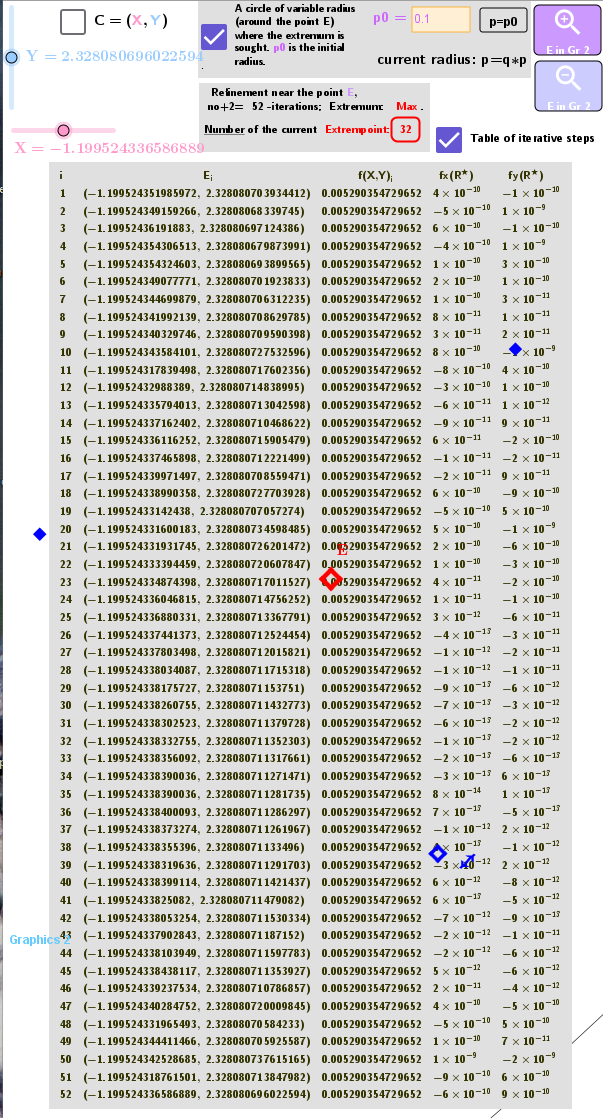
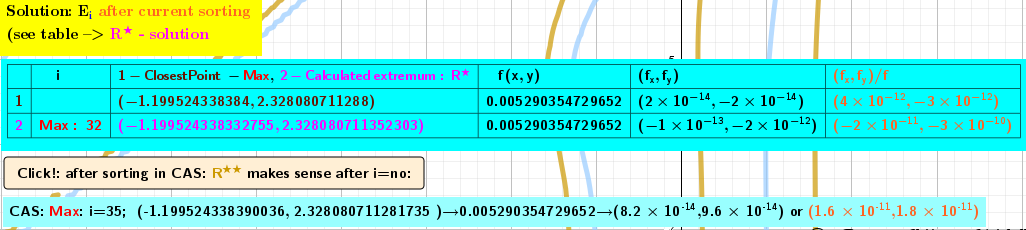
The number of iteration steps is no. Here, it should be taken into account that at the points (X,Y) of the iteration, the values of the function f(X,Y) are close to each other and the choice of the maximum/minimum value (here they are estimated parameters) from the function values is at the limit of the accuracy of the GeoGebra algebra. That is, the best element is not necessarily the last member of the iteration. Therefore, the "best" point is constantly (at each iteration step) determined by sorting. R*: Step i=32.
And in order to "improve the result", all iteration points at the end of the calculation are checked using CAS, where the accuracy of the calculations is much higher. R**: Step i=35. Interestingly, the functions of the sorting points are always in the interval of the current iteration.
The values of the partial derivatives fx and fy for the functions under consideration for a point sorted in this way give zero values with high accuracy!