Chebyshev Linkage Wheel
This apparatus is a square wheel made by Chebyshev Linkage (approximate straight-line mechanism).
In figure, the solid-line bars are components of this apparatus. The dashed-lines are explanatory lines.
Aqua-colored big bullet ● E is a axis of this wheel.
This apparatus has beautiful property.
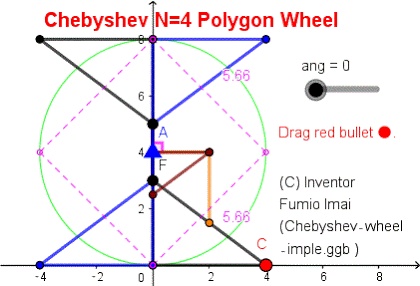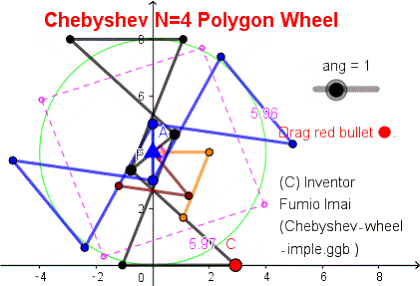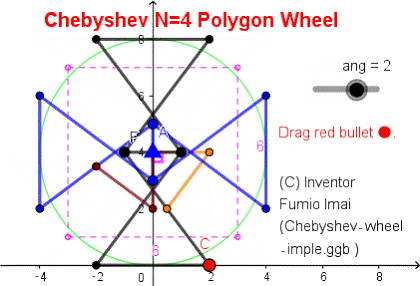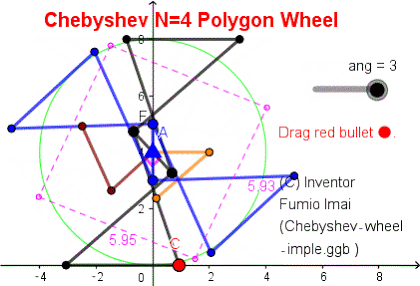
① ABCD (= #1) is a basic component.
AB = Lower base (length 4), AD or BC = Cross-oblique sides (length 5), CD = Upper base (length 2).
(We suppose that AD and BC are always crossed. To avoid the uncrossed situation , we must attach the angle limitation stopper. i.e. Keep BP ≧ 0.)
This apparatus has 4 components (#1,#2,#3,#4). #1 and #3 are point-symmetry each other. #2 and #4 are, too.
② #1 and #2 (LM, ON) position relation has next rule.
a) Lower base ⊥ others Upper base.
From a), ON (#2 Upper base) is always vertical. ∵ AB is fixed and horizontal.
From a), LM (#2 Lower base) is rotate 0 to 180゜. ∵ CD rotates 180゜.
[ In same component, Lower and Upper bases move alternately each other. i.e. When one is rotating, the other is not-rotating. ]
Rule a) is established by various ways, but, the most simple way is used in above figure.
i.e. R = the middle of BC (length 2.5 [= 5/2] ), Suppose S , RS = length 2.5, ES= length 2 [= 4/2].
From theoretical analysis, ES // AB. --- so, To make ON ⊥ AB is equivalent to to make ON ⊥ ES.
(We can reduce the number of bar by this way.)
At the end, Force to fix the angle between ES and ON toward 90゜. --- welding/ glue.
In real implementation, prepare short macaroni tube== (plural pasrts),
And insert axis bar --- into it.
as --==---==---==---==---. ← 4 macaroni.
Axis design: ---- Implementation is easy. ( #1 is independent, others are all dependent.)
#1/#3 upper-bar ① ---- == macaroni_1 (bonds with naked Axis-bar ---)
#1/#3 lower-bar ES ② ---- == macaroni_2
#2/#4 upper-bar ③ (⊥ with ②) ---- == macaroni_3 (bonds with macaroni_2)
#2/#4 lower-bar EU ④ (⊥ with ①) ---- == macaroni_4 (bonds with naked Axis-bar ---)
Chassis (car_body) ---- == macaroni_5
[ i.e. The smallest configure is ------==-- style. With only one macaroni. ]
I think this inventions is a home-run hit in the human being history.
(This figure was made by GeoGebra Graphics View's copy-function. GeoGebra is powerful educational tool.)
★ Feeling.
Please imagine, there exists vertical real gravity ↓ [vector ON], so, ground AB is horizontal.
upper base CD vector is 2nd. virtual gravity →, so, #2 Lower base MO' ⊥ CD.
virtual gravity rotates, in last, it directs to real gravity direction. and, it will be baton touched/ passed.
■ Easy making (??) ---- This is a kind of instant wheel.
1. Prepare 2 sets of Chebyshev point-symmetry linkages.
2. Prepare one axis bar.
3. Insert the axis bar into 2 each symmetry points. Here, axis bar is like a BBQ skewer.
4. attach the rule a) cordinator 3 bars (2.5, 2.5, 2 length bars) between to 2 point-symmetry linkages.
5. Set 90° adapter (corresponds to α = 90° mechanism ).
■ About practical utility :
・ wheel for on a sand-beach, carpet (----- small loss caterpillar. )
・ caster of travel bag
・ instant wheel ( They are only bars, usually.)
・ heavy weight lifting wheel/ roller (constant height)
cf. Monster 4x4 Mud Trucks at Good Time 4x4's June 12Th 2011 (YouTube) ---- interesting vtr.
★ Variant :Q: Please consider Hexagon (= 6 edges) wheel. 3 sets of the point symmetry Chebyshev frame.
A: It's easy. ---- rule a') Lower base ∠60° & ∠120° other 2 Upper bases.
(2 grounded foot width is narrow than 4 edgee case.)
cf. Chebyshev Linkage Wheel2
■ Pedal driven implementation FIG.
Below pink square is available to make a pedal crank mechanism.