Aproximação do raio da Terra
Aproximando o planeta Terra por uma esfera e utilizando as ideias da Geometria Esférica, podemos calcular o seu raio. Isso foi feito por Eratóstenes de Cirene (276 a.C. - 194 a.C.). Eratóstenes descobriu que, ao meio dia, o Sol formava o que parecia ser um ângulo reto com o solo em um poço da cidade de Siena, de modo que era possível observá-lo do fundo do poço. Em Alexandria, no mesmo horário, Eratóstenes cravou uma estaca perpendicular ao solo e mediu o ângulo formado entre os raios solares e a estaca.
Para isso, é possível calcular o arco cuja a tangente é a razão entre o comprimento da sombra e o tamanho da estaca. Assim, Eratóstenes obteve . Como os raios do Sol são paralelos, então o ângulo formado entre o poço em Siena e a estaca em Alexandria é o mesmo ângulo medido por Eratóstenes. Veja a figura a seguir (sem escala):
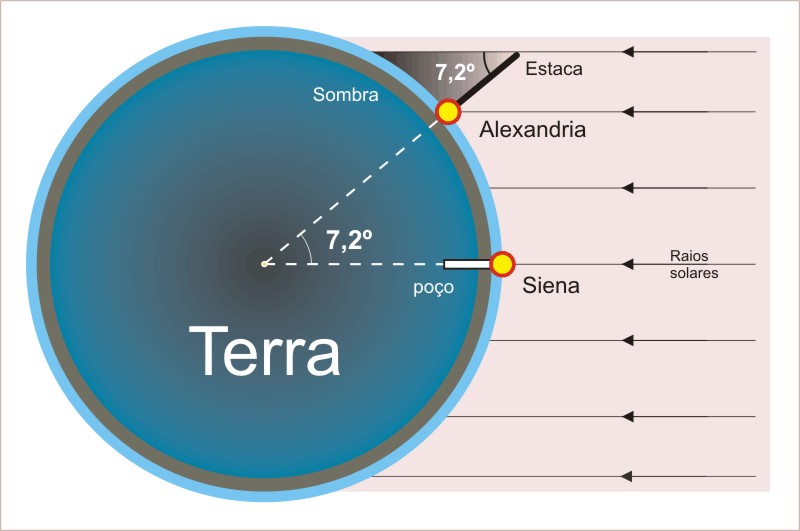
Fonte: http://www.ime.unicamp.br/~apmat/a-primeira-medicao-do-raio-da-terra/#:~:text=Hoje%2C%20sabe-se%20que%20o,km%20da%20medida%20de%20Erat%C3%B3stenes. Assim, basta saber a distância entre o poço em Siena e a estaca em Alexandria. Usando a unidade da época, Eratóstenes encontrou 5000 estádios. Cada estádio vale cerca de 157 metros, ou seja, a distância entre as duas cidades era de 785 quilômetros, aproximadamente. Fazendo uma regra de três, obtemos a circunferência da Terra: Usando uma aproximação para o número , que já era conhecido entre os gregos, obtemos . Atualmente se estima o raio da Terra em 6370 quilômetros, o que mostra uma boa estimativa de Eratóstenes, você não acha?