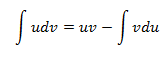Integración por partes
1. El método
El cálculo de primitivas puede ser complicado en ocasiones, por lo que disponemos de diferentes métodos de integración que nos ayudan en este tarea. Uno de ellos es la integración por partes, útil, sobre todo, cuando tenemos en el integrando un producto o un cociente. Este método se basa simplemente en la fórmula
Identificamos en nuestra integral los factores y y aplicamos la fórmula. Para obtener tenemos que derivar y para obtener tenemos que integrar . Por tanto, la dificultad del método radica en la buena elección de los factores y para poder derivarlo e integrarlo, respectivamente.
2. Ejemplo de aplicación paso a paso
Podemos escoger entre
y
Notemos que ahora tenemos que calcular una integral más complicada que la inicial. Esto se debe a que en el primer caso disminuimos el grado del polinomio al derivar, mientras que en el segundo lo aumentamos.
3. Ejemplo de aplicación 2
4. Otros ejemplos