Monte-Carlo-Methode am Vollkreis
Monte-Carlo ist ein Stadtbezirk in Monaco . Bekannt ist er für die gleichnamige Spielbank und die alljährlich stattfindende Rallye Monte Carlo. Auch der Circuit de Monaco, auf dem der Große Preis von Monaco ausgetragen wird, führt zum Teil durch Monte-Carlo.
Die Monte-Carlo-Methode, ist ein Verfahren bei dem mit einer großen Anzahl an gleichartiger Zufallsexperimente versucht wird, nur aufwendig lösbare Rechen-Probleme über das Zählen zu lösen. Als Grundlage ist vor allem das Gesetz der großen Zahlen zu sehen, demzufolge sich bei eine ausreichend viele Zufallsexperimenten einigermaßen genau bestimmen lässt, wie groß eine Wahrscheinlichkeit für ein bestimmtes Ereignis ist.
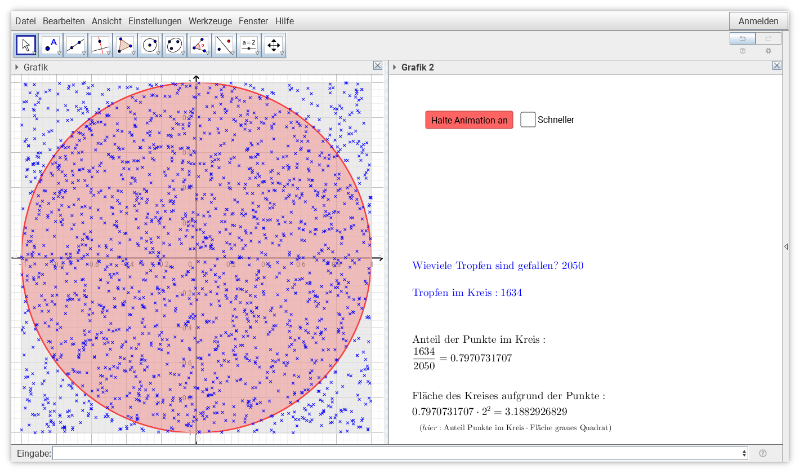
Bei der Kreisberechnung geht es um die Wahrscheinlichkeit, mit der ein zufälliger "Regentropfen" (= Punkt) in einem Kreis erscheint, wenn man "Regentropfen" (= Punkte) auf ein Quadrat fallen lässt. Natürlich zählt man keine echten Regentropfen, sondern lässt per Zufall Punkte erzeugen.
Die Wahrscheinlichkeit bzw. der Anteil der Punkte im Kreis im Vergleich zu der gesamten Punkte-Anzahl gibt an, wie groß die Fläche des Kreises im Vergleich zur Fläche des Quadrates ist.
Beschreibung des GeoGebra-Arbeitsblatt (zuerst nur ein Bild!)
Links sieht du den Bereich, in dem die Punkte, deren Koordinaten per Zufall erzeugt wurden, angezeigt werden.
Rechts findest du Zahlen, etwa wie viele Punkte es schon geregnet hat und wie viele davon im Kreis liegen. Unten steht auch wie groß der Anteil der Punkte im Kreis liegen im Vergleich zu der Gesamtanzahl. Da hat man immer einen Bruch/eine Zahl kleiner als 1.
Das graue Quadrat hat die Fläche 4, denn seine Seitenlänge ist 2. Mit dem Bruch kann man dann abschätzen, wie groß die Fläche des Kreises ist, wenn man den Bruch als Anteil der Größe vom Quadrat betrachtet.
Im ersten Durchgang, werden 2000 Punkte erzeugt, später kannst du auch eine größere Anzahl ausprobieren oder noch einmal 2000 Punkte erzeugen lassen.
Aufgabe
Probiere nun die Simulation aus, die nach diesem Text folgt.
Stelle deinen Mitschüler vor, was die Zeichnung macht und erkläre, wie man dadurch auf die Fläche von einem Kreis kommt.
Bevor du es vorstellst, solltest du dich bei mir melden und Fragen klären, damit du auch sicher die richtigen Informationen an die Mitschüler weitergibst.