Função Quadrática
Definição
Toda funçãoestabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números
reais e a ≠ 0, é denominada função do 2º grau.
Propriedades Gráficas
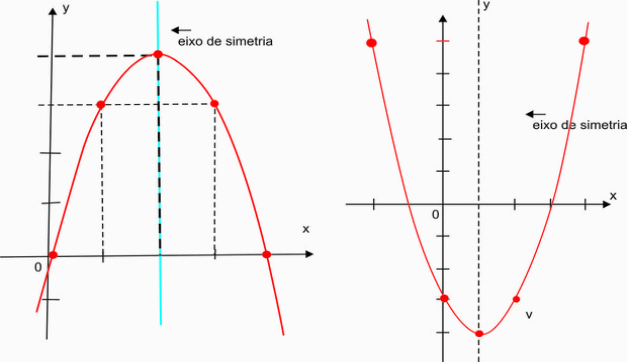
O gráfico da FunçãoPolinomial do 2º Grau y = ax2 + bx + c é uma parábola cujo eixo de
simetria é uma reta vertical, paralela ao eixo y ou até mesmo o próprio eixo y,
passando pelo vértice da parábola.
Raiz da Função
Determinar a raiz de uma função é calcular os valores de x quesatisfazem a equação do 2º grau ax² + bx + c = 0, que podem ser encontradas
através do Teorema de Bháskara:
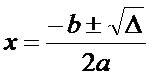
Número de raízes reais da função do 2º grau
Dada a função f(x) =ax² + bx + c, existirão três casos a serem considerados para a obtenção do
número de raízes. Isso dependerá do valor do discriminante Δ.
1º caso → Δ > 0: A funçãopossui duas raízes reais e distintas, isto é, diferentes.
2º caso → Δ = 0: A função possui raízes reais eiguais. Nesse caso, dizemos que a função possui uma única raiz.
3º caso → Δ < 0: A função não possui raízesreais.
Soma e produto das raízes
Seja a equação, ax² +bx + c = 0, temos que:
Se Δ ≥ 0, a soma das raízes dessa equação é dada por
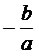
e o produto das raízes por
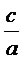
De fato, x’ e x’’ são as raízes da equação, por isso temos:
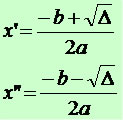
Soma das raízes
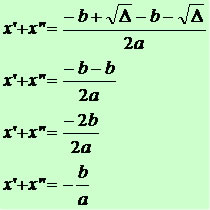
Produto das raízes
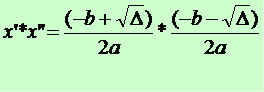
Efetuando a multiplicação, temos:
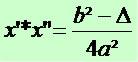
Substituindo Δ por b² – 4ac, temos
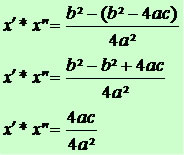
Após a simplificação, temos:
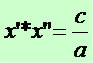
Aplicações da Função Quadrática em nosso dia a dia
Há várias situações na vida real em que a configuração de arco da parábola está presente:
Pontes Penseis
Parábolas são utilizadas na engenharia na construção de pontes estáveis e econômicas, sendo que todas elas são de formato
parabólico.
Faróis dos carros
Os faróis dos carros possuem,respetivamente uma lâmpada que é colocada no foco da superfície parabólica.
Neste caso podemos ter acesso às propriedades óticas da parábola.
Antenas Parabólicas
São objetos bastante utilizados nas comunicações atuais, através de transmissão ia satélite, telefonia móvel e GPS-sistema de radionavegação baseado em satélites.