Rectas de colores
El color dinámico puede ser una gran herramienta en la exploración de lugares geométricos o en la investigación de curvas algebraicas, diagramas de Voronoi y en otros campos que quizás aún estén sin explorar, sin embargo, en este artículo nos centraremos en tareas más sencillas.
Comenzaremos con un tarea muy simple que desembocó en lo que yo denomino Arte con Geogebra. Allá por el año 2011 se celebró en Gijón las XV JAEM, entre las múltiples actividades programas hubo un espacio de debate sobre Geometría Dinámica conducido por José Antonio Mora. Allí presenté una trabajo realizado con alumnos. Una muestra de los trabajos se puede ver en https://multiplicateporcero.wikispaces.com/Arte+geogebra y en https://estoestodoamigos.wikispaces.com/Arte+Curvo.
Después José Antonio Mora, en el día GeoGebra 2012 presentó un taller de rectas y curvas de colores, un estupendo trabajo de aula donde amplió de forma extraordinaria la idea de los colores dinámicos. La idea original consistía en representar una recta y=m x + n, con m y n dos deslizadores y aplicar los colores dinámicos a la recta según los valores de m y n.
Veamos cómo.
Guía de construcción. Recta de colores
- Creamos dos deslizadores m y n que serán la pendiente y la ordenada de la recta. Los valores máximos y mínimos los dejamos por defecto y cambiaremos el incremento a 0.001.
- Hacemos clic en la vista gráfica 1, a continuación escribimos en la barra de entrada: y= m x + n.
- En la ventana propiedades de la recta, pulsamos en la pestaña Avanzado y escribimos tres funciones que contengan como parámetros a m y n.
- Antes de cerrar la ventana propiedades, en la pestaña básico activamos el rastro.
Ejemplo de configuración de colores.
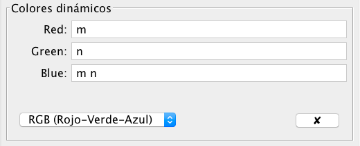
- Cuestiones
- Activa la animación del deslizador m. Describe que sucede.
- Activa la animación del deslizador n. Describe que sucede.
- Cambia la expresión de los colores. Realiza tu propia composición.
- Ahora para el deslizador n y deja que solo se mueva el deslizador m.
- ¿Por qué las rectas más inclinadas están más juntas y las que tienen menor inclinación están más separadas? Fíjate en la ilustración 8, que eso ocurre tanto cuando la inclinación es positiva como cuando es negativa y además para cualquier valor de la ordenada en el origen.undefined
Ilustración 8
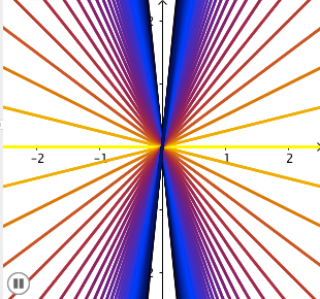
Observa la siguiente imagen:
![Intenta reproducirla. Usa tus propios colores.
[list]
[/list]](https://www.geogebra.org/resource/XaRXbj3u/lym6Yi4sHFobzaKT/material-XaRXbj3u.png)