Sum of geometric series (AA SL 1.8, AI HL 1.11)

Keywords

English	Japanese	Korean	Chinese Simplified
Infinite Geometric Series	無限等比級数	무한 등비급수	无限等比级数
Sum Formula	和の公式	합 공식	求和公式
Convergence	収束	수렴	收敛
Common Ratio	公比	공비	公比
Divergence	発散	발산	发散
Asymptotic Behavior	漸近的な振る舞い	점근적 행동	渐近行为
Sum to Infinity	無限大の和	무한대의 합	无穷和
Geometric Progression	等比数列	등비수열	等比数列
Limit	極限	한계	极限

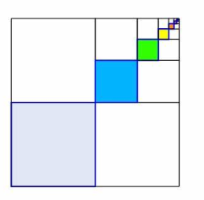
Factual Questions	Conceptual Questions	Debatable Questions
1. What is the formula for the sum of an infinite geometric series?	1. Why does the sum of an infinite geometric series only converge for \|r\| < 1?	1. Is the concept of infinite geometric series more abstract than that of finite geometric series?
2. Calculate the sum of the infinite series 0.5 + 0.25 + 0.125 + ...	2. Explain how the formula for the sum of an infinite geometric series is derived.	2. Can the concept of infinite geometric series be effectively applied in real-world scenarios?
3. Under what condition does an infinite geometric series converge?	3. Discuss the concept of convergence and divergence in the context of geometric series.	3. Debate the importance of understanding infinite series in the broader context of mathematics.
4. Find the sum of the infinite geometric series 3 + 1.5 + 0.75 + ...	4. How does changing the first term of an infinite geometric series affect its sum?	4. Discuss the statement: "The sum of an infinite series challenges our conventional understanding of infinity."
5. What is the common ratio in the series 2 + 6 + 18 + 54 + ...?	5. Compare the behavior of convergent and divergent geometric series.

Mini-Investigation: The Geometric Series JourneyWelcome to the Geometric Series Journey, a numerical adventure to understand the power of multiplication and addition! Let's dive into the realm of geometric progression with a playful exploration. Chart your discoveries and share them with other math explorers.

1. Starting Strong: Our series starts with a first term, , of 50 and a common ratio, , of . What happens to the terms of the series as we progress? Predict the 10th term without peeking and then check!

2. Ratio Riddles: Change the common ratio to . How does this affect the progression of our series? Do the terms increase or decrease? Test your hypothesis and observe the new graph.

3. Summing It Up: Look at the summation table. Notice how the sum, Sₙ, increases as n gets larger. What do you think the sum would be after terms? After terms? Take a guess and then use the applet to find out.

4. Asymptotic Adventures: The graph seems to approach a horizontal dashed line as n increases. Can you guess the value it's approaching? Hint: There’s a formula for the sum of an infinite geometric series!

5. Break the Bank: Suppose you start with 50$ and keep adding 90% of the previous amount you added. How much money will you have after 10 additions? Does this match with the applet's Sₙ for n=10?

6. Limit Quest: If the common ratio is between -1 and 1, the series has a limit. What happens to the series when the common ratio is outside this range? Experiment and document the results.

7. Common Ratio Conundrum: What if the first term stays the same, but you can choose any common ratio? Find a ratio that gives you a sum as close to 500 as possible without going over, in the first 10 terms.

8. Negative Notions: Change the common ratio to a negative value, like -0.9. How does the sign of the ratio affect the series? Observe the graph and summarize your findings.

9. Geometric Growth: How would you describe the growth of a geometric series to a friend who’s never seen one before? Think of a real-world example that illustrates this concept.

10. Infinity Inquiry: The applet allows us to see the sum of finite terms. But what does it mean to sum an infinite geometric series? Can you have an infinite sum that’s a finite number?

Part 2 - Checking for understanding Watch the below video before attempting the quiz questions