Una demostración del Teorema
La primera versión escrita de este teorema se encuentra en "The Ladies' Diary", “El Diario de las Damas”, planteada en 1825 por un matemático inglés, Dr. W Rutherford, en el Nº 122, dentro de la sección de “Nuevas Cuestiones Matemáticas” -cuestión VII- página 47 donde se proponía esta cuestión para que el lector diera una demostración.
Este “diario” o “almanaque de la mujer” apareció en Londres en 1704, con una periodicidad más o menos regular hasta 1841. En él se presentaban adivinanzas, llamados “enigmas”, jeroglíficos, consultas científicas, información sobre la salida y la puesta de sol, las fases de la luna, días de fiesta, eclipses, rompecabezas, cuestiones matemáticas en verso.
En algunos volúmenes se incluían preguntas y respuestas propuestas por los lectores. Una de ellas fue la demostración al Teorema de Napoleón y que aparece publicada en 1826 en el Diario de las Damas
cuestión VII, página 38.
Guía de una demostración
La primera demostración es la respuesta dada por Mr. Tho, Burn de Woodburn y Mr. John Walker, West Boldon a la cuestión planteada un año antes por Rutherford. Está basada en triángulos semejantes. Traducimos la demostración íntegramente.
Únicamente la anotación entre corchetes azules no apareció en la publicación original
- Sean ABC un triángulo
- AGB, BHC, CKA triángulos equiláteros descritos sobre los lados del triángulo
- D,E,F son sus centros de gravedad
- Unimos los segmentos FD, DE, EF, FA, AD, DB, BE, AH, y BK
- El ángulo ACK= ángulo BCH
- Añadiendo el ángulo ACB a los dos anteriores tenemos que el ángulo BCK=ángulo ACH
- Pero los lados AC y CH son iguales a los lados KC y CB respectivamente
- Deducimos que los triángulos BKC y AHC son iguales
- AH=BK con lo que se deduce la proporcionalidad de BD, BE, respecto a L y M
- Entonces desde D, E, que son centros de gravedad de los triángulos equiláteros ABG y CBH, es bien conocido el siguiente hecho: Ángulo ABL= Ángulo CBM= 1/2 · Ángulo ABC= 1/2 · Ángulo CBH= 30º
- Sabemos que [BL y BM son las medianas] BD=2/3 · BL y BE=2/3· BM
- Lo que hace que los triángulos BCM, ABL sean semejantes.
- Además se puede visualizar que: Ángulo CBE+Ángulo ABD=Ángulo CBH
- Tenemos que Ángulo DBE=Ángulo ABH.
- Entonces los triángulos DBE y ABH son semejantes.
- De la misma manera AKB y ADF son semejantes de donde se deduce que DE=DF
- Análogamente DF=FE por tanto el triángulo DEF es equilátero. Como queríamos demostrar.
- “la demostración se aplicará cuando los vértices G, H, K son girados hacia el centro”
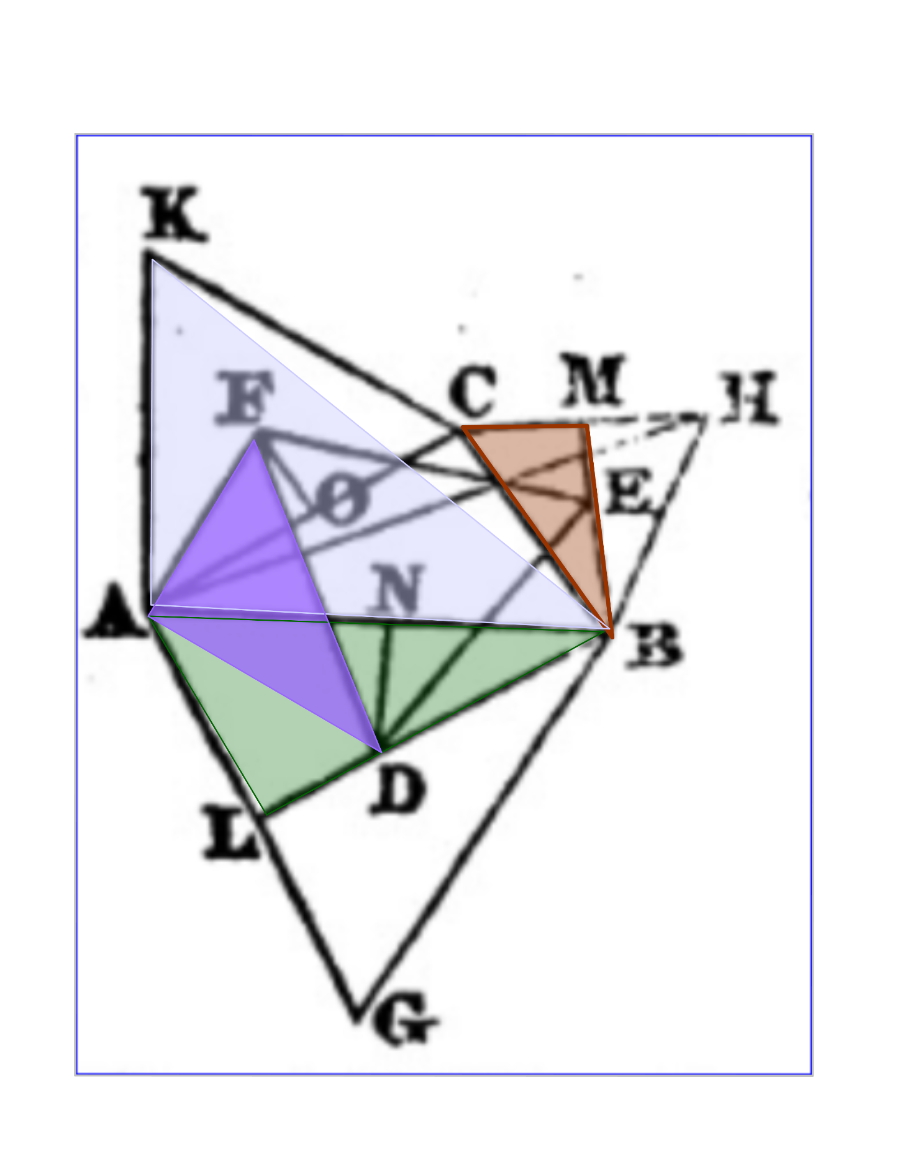
Demostración de 1826 publicada en el Diario de las Damas.
