Kapitel
Analytic Geometry. 14 propositions after D.Beklemishev
The introduction
“Mathematics is the part of our culture that has investigated algorithmic thought in the most profound and systematic way. Now mathematics has a great deal to say about algorithmic thought” (Byers, 2007). In fact, the question “Is thought algorithmic?” could be replaced by “Can a computer do mathematics?” or “Is mathematics algorithmic?” What aspects of mathematical activity can computers duplicate? Consider the relationship between computing and mathematics, between mathematical thought and computer simulations of thought processes. Normally using mathematics to investigate some subject means creating a mathematical model, using mathematical techniques to draw out the mathematical consequences of that model, and, finally, translating the conclusions back to the original situation.
Due to its possibility of using the algorithmic approach the package GeoGebra was chosen as the assistant for the students of the computer science faculty in their learning of analytic geometry. The main idea was to detect a gradual increase in students’ level (for the students, who mostly use mathematics instrumentally) from remembering and understanding till applying, analyzing, evaluating, and creating.
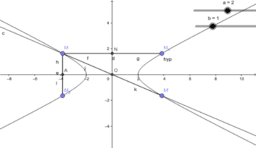
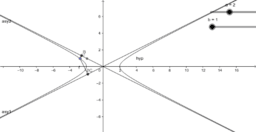
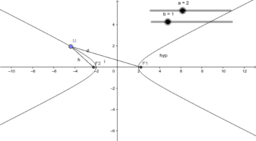
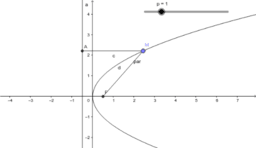
We consider the propositions (1987) of different complexity levels from the course of analytic geometry. Beklemishev D.V. states that he geometric properties of the three second order lines are not obvious. They are ellipse, hyperbola and parabola.
Byers W. (2007) How mathematicians think: using ambiguity, contradiction, and paradox to create mathematics. Princeton, New Jersey
Beklemishev D.V. (1987) The course of analytical geometry and linear algebra. Moscow. (In Russian)