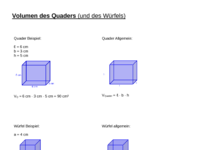
Volumen eines Quaders
Aufgabe 1
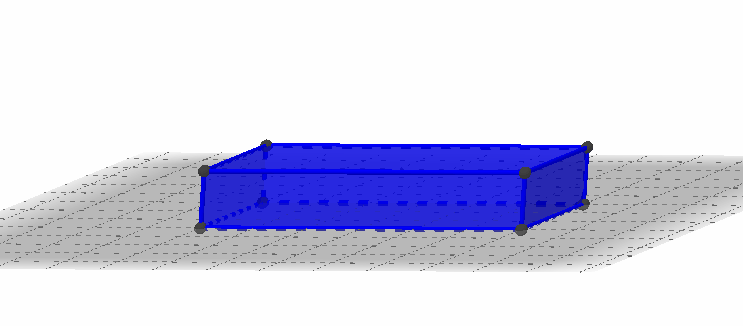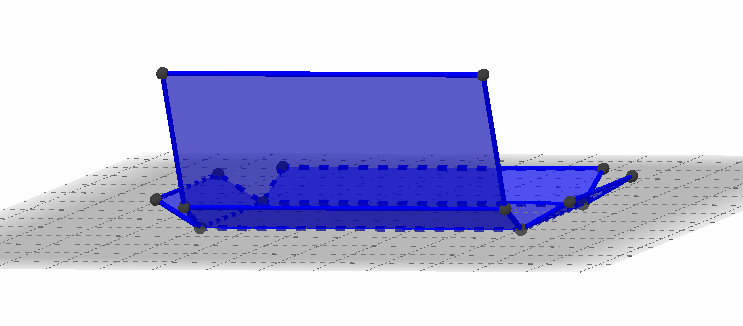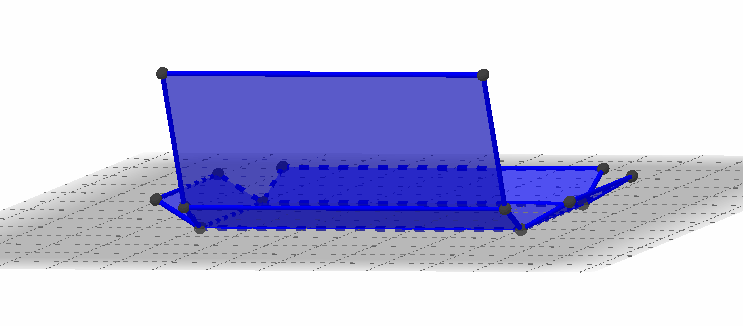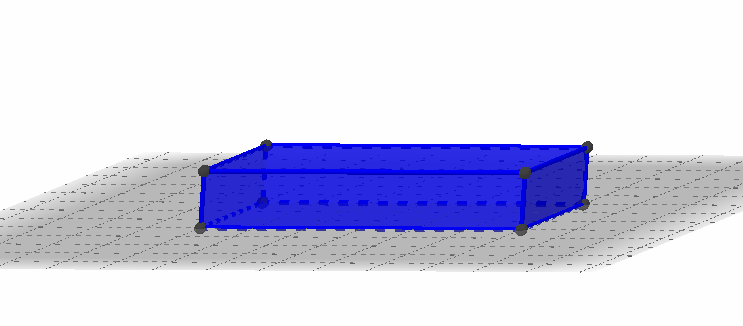
Die quaderförmige Box ist 6 cm lang, 3 cm breit und 1 cm hoch.
Wie viele Einheitswürfel mit Kantenlänge 1 cm passen in die Box?
Aufgabe 2
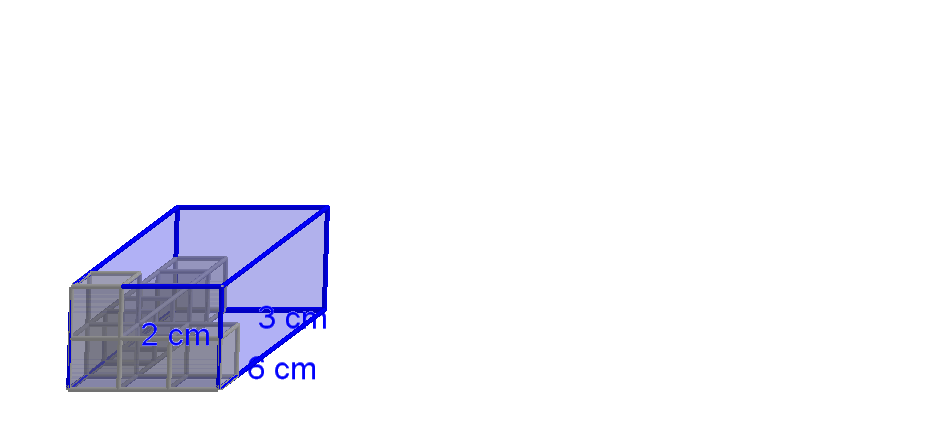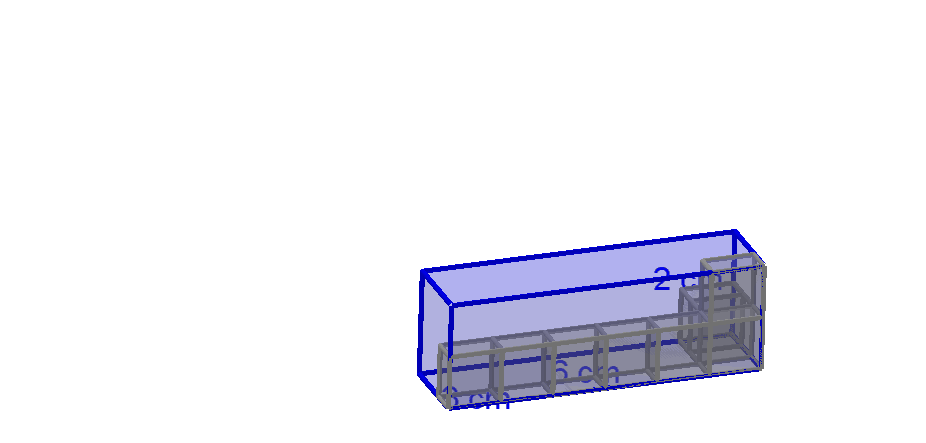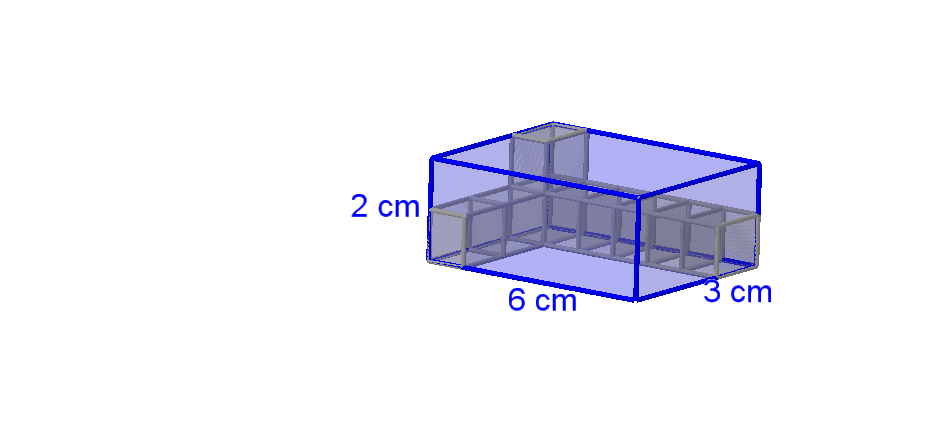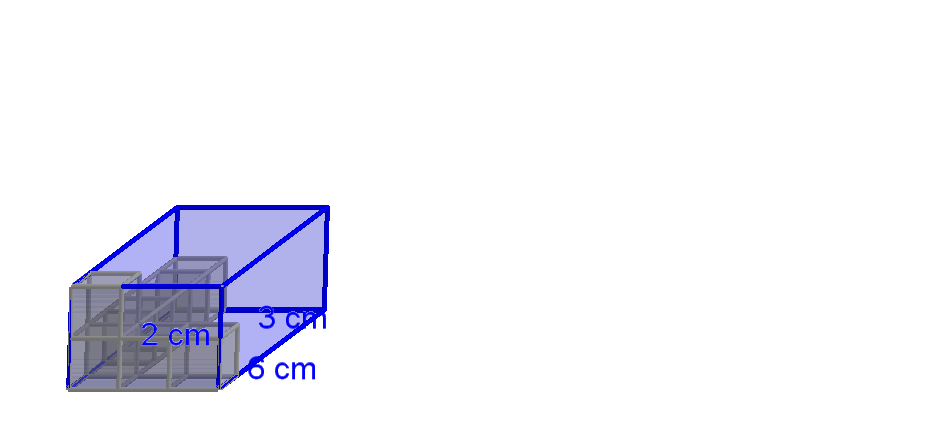
Die quaderförmige Box ist 6 cm lang, 3 cm breit und 2 cm hoch.
Wie viele Einheitswürfel mit Kantenlänge 1 cm passen in die Box?
Erklärung
Der Einheitswürfel hat die Kantenlänge 1 cm.
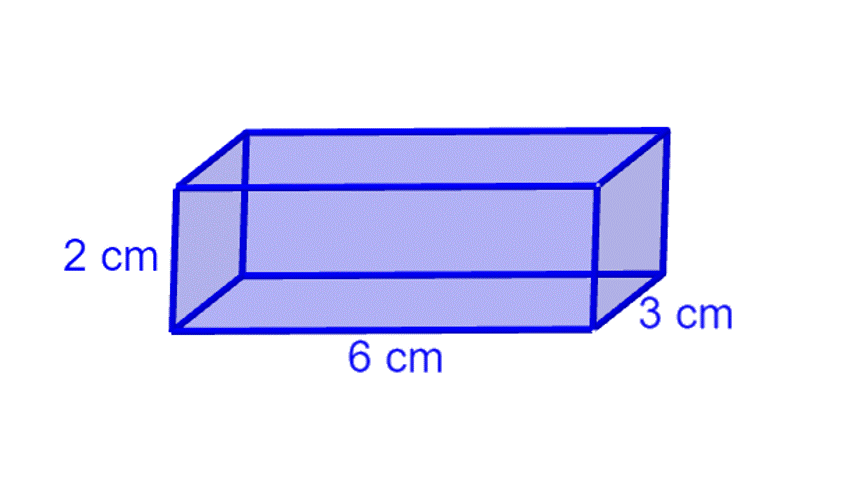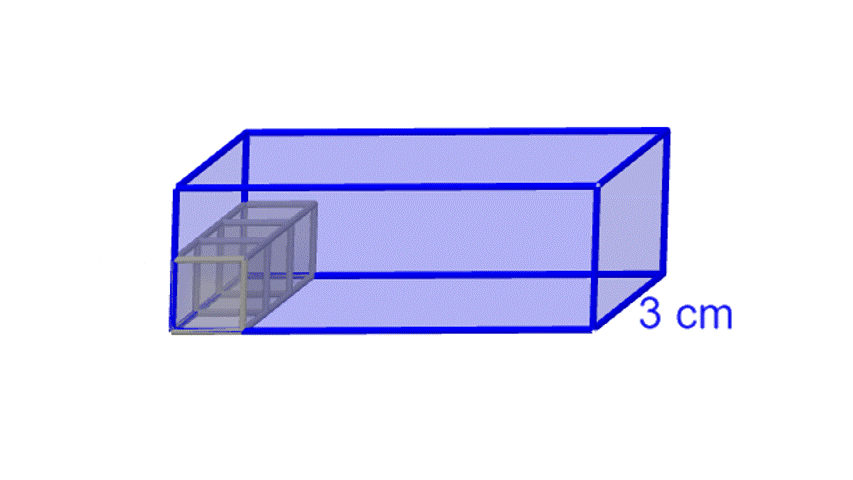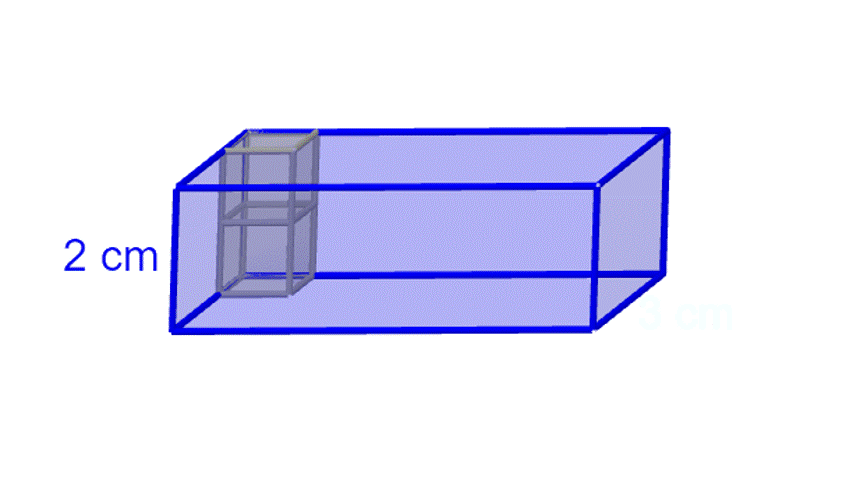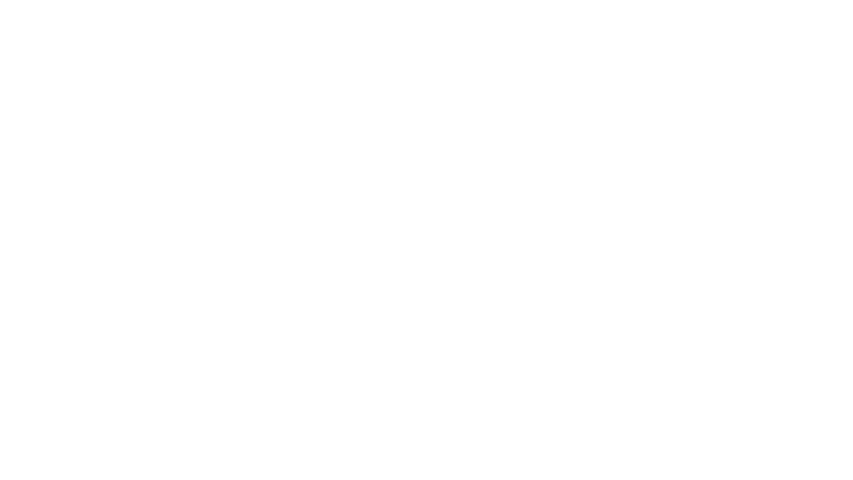
Wir betrachten die quaderförmige Box mit
Länge l = 6 cm,
Breite b = 3 cm und
Höhe h = 2 cm.
- Anzahl der Einheitswürfel, die in die Länge der Box passen: 6
- Anzahl der Einheitswürfel, die in die Breite der Box passen: 3
- Anzahl der Einheitswürfel, die in die Höhe der Box passen: 2
"Kenne ich also die Maße eines Quaders in cm, dann kann ich einfach den Rauminhalt V des Quaders berechnen, zum Beispiel .
Ich merke mir: Volumen eines Quaders ist Länge mal Breite mal Höhe"
36 cm³ ist das gleiche Volumen, das 36 Einheitswürfel besitzen!
(Begründung: der Einheitswürfel ist ein Quader mit l = 1 cm, b = 1 cm und h = 1 cm, also .)
Übernimm den Hefteintrag: