a new hexagonal 3-web of circles

Autor:
Walter Füchte

Diese Seite ist Teil des GeoGebra-Books Moebiusebene. (20. Juli. 2022) Diese Seite ist auch eine Aktivität des Geogebra-Books Sechseck-Netz

Unten: Dies ist kein Applet, sondern ein Bild des Applets auf der nächsten Seite! Wegen eines hohen Aufwands an Rechnungen sind die Lade-Zeiten sehr lang. Das Applet funktioniert dennoch!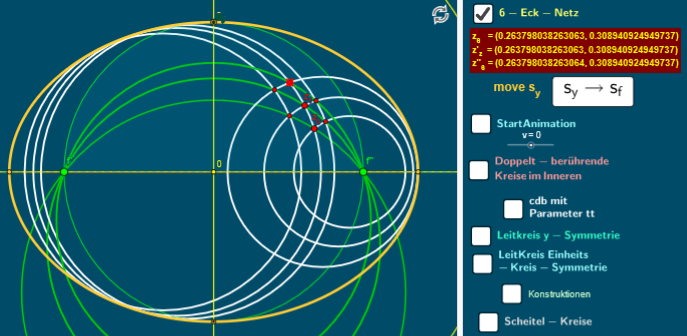
Image
Die im Inneren einer bizirkularen Quartik doppelt-berührenden Kreise erzeugen mit den Kreisen durch die im Inneren liegenden Brennpunkte dann und nur dann ein 6-Eck-Netz aus Kreisen, falls der zur Symmetrie-Achse symmetrisch liegende Kreis durch die Brennpunkte zugleich ein Scheitelkreis ist. Dieses 6-Eck-Netz ist nach unserem Wissensstand bisher unbekannt. Erklärungen und Berechnungen: 2-teilige bizirkulare Quartiken besitzen 4 paarweise orthogonale Symmetrie-Kreise; auf einem dieser Symmetriekreise liegen die 4 Brennpunkte . Wählt man die Koordinatenachsen und den Einheitskreis als Symmetrie-Kreise, ergeben sich die Brennpunkte und die Quartiken implizit durch Gleichungen des Typs:
Die Brennpunkte können auf 3 Weisen als Grundpunkte zweier elliptischer Kreisbüschel dienen. Die Quartik ist Winkelhalbierende der sich auf der Quartik schneidenden Kreise aus den Kreisbüscheln. Symmetrisch zu diesen Kreisen liegen die doppelt-berührenden Kreise, aus welchen W. Wunderlich 1938 "besondere Dreiecks-Netze aus Kreisen" konstruiert hat. Diese doppelt-berührenden Kreise können einfach mit Hilfe der zugehörigen Leitkreise konstruiert werden. Die Leitkreise ermöglichen auch die Konstruktion der doppelt-berührenden Kreise durch vorgegebene Punkte, und damit die "Konstruktion" der genannten Dreiecks-Netze.
Wie konstruiert man die -achsensymmetrischen doppelt-berührenden Kreise? Für die achsensymmetrischen doppelt-berührenden Kreise nützen die Leitkreise wenig. Wir untersuchen die hyperbolischen Kreisbüschel um die Brennpunkts-Paare f , f' bzw. f'' , f'''. Für diejenigen Brenn-Kreise aus den beiden Kreisbüscheln, die sich auf der Quartik schneiden, ist die Quartik wieder Winkelhalbierende, die gesuchten doppelt-berührenden Kreise sind Symmetrie-Kreise der Brenn-Kreise. Die Konstruktion beruht auf einer einfachen Eigenschaft der Brenn-Kreise:
  • Spiegelt man einen der Achsenschnittpunkte des einen Brenn-Kreises an einem Scheitel-Kreis, so erhält man einen Achsenschnittpunkt des anderen Brenn-Kreises.
Diese Eigenschaft findet man auch bei den Kegelschnitten wieder: die Brenn-Kreise sind konzentrische Kreise um die Brennpunkte (der 2.-te Brennpunkt ist !) Man berechnet die Parameter der Brenn-Kreis-Schnittpunkte mit der -Achse:
  • mit , spiegle an , ,
und daraus die Kreis-Gleichungen: : und : Die Berechnung der Schnittpunkte ergibt eine Parameterdarstellung der bizirkularen Quartik:
  • und
Aus Symmetrie-Gründen berechnet sich hieraus der Mittelpunkt des doppelt-berührenden Kreises, welcher Symmetrie-Kreis der beiden Brenn-Kreise ist_
und dazu den Radius
Für die Frage, ob ein 6-Eck-Netz aus den angegebenen Kreisen erzeugt werden kann, hat man die doppelt-berührenden Kreise durch einen vorgegebenen Punkt zu bestimmen: man löse die Gleichung nach t auf:
Wenn es Lösungen gibt, gibt es immer genau 2 Lösungen, auch wenn die komplizierten Gleichungen nicht wie quadratische Gleichungen erscheinen wollen! Die Berechnungen oben wurden händisch durchgeführt, das geogebra-CAS war keinerlei Hilfe. In den nachfolgenden Applets wurden die Lösungen mit geogebra-Lösungen(gleichung) berechnet. Die Folgen sind einerseits die langen Ladezeiten der Applets, andererseit die wirklich überraschenden übereinstimmenden Schnittpunkts-Berechnungen bis fast zur 15-ten Nachkommastelle, falls ein 6-Eck-Netz vorliegt! Der vorliegende neue Fall eines 6-Eck-Netzes aus Kreisen ergänzt die Beispiele F N (e) von FEDOR NILOV und Ein neues 6-Eck-Netz aus Kreisen 2.

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen