Volúmenes de figuras

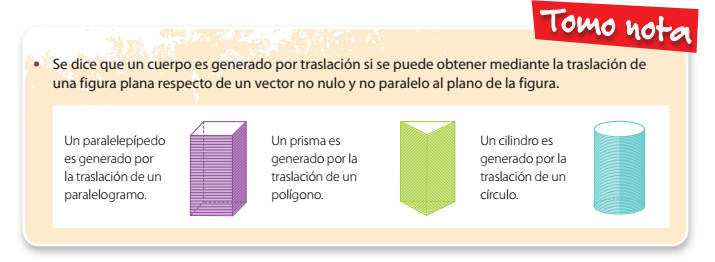
Cuerpos generados por rotación o traslación

Aprenderé a: identificar cuándo se dice que un cuerpo está generado por rotación o por traslación. Relacionar la figura plana con el cuerpo correspondiente generado por rotación o por traslación. Esbozar el sólido de revolución a partir de la figura plana que lo genera. Reconocer la figura plana a partir del sólido de revolución generado.

En general, se denominan cuerpos generados por rotación o sólidos de revolución aquellos que pueden obtenerse mediante la rotación de una curva alrededor de un eje. A dicha curva se le llama generatriz. En este sentido, la esfera es un cuerpo generado por rotación, su generatriz es la circunferencia y su eje es el diámetro de la circunferencia, ya que, tal como se puede apreciar en las imágenes, al girar una circunferencia en torno a su diámetro, se observa una esfera.

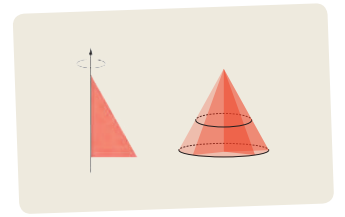
De manera similar, si se gira un rectángulo en torno a uno de sus lados, se puede
observar un cilindro, mientras que si se gira un triángulo rectángulo en torno a uno
de sus catetos, se puede observar un cono. — De manera similar, si se gira un rectángulo en torno a uno de sus lados, se puede observar un cilindro, mientras que si se gira un triángulo rectángulo en torno a uno de sus catetos, se puede observar un cono.

Otro ejemplo de cuerpo generado por rotación es el tronco de
un cono o cono truncado. Este se genera mediante la rotación del
trapecio rectángulo ABCD cuyo eje corresponde al lado BC, como
muestra la figura — Otro ejemplo de cuerpo generado por rotación es el tronco de un cono o cono truncado. Este se genera mediante la rotación del trapecio rectángulo ABCD cuyo eje corresponde al lado BC, como muestra la figura

Al realizar la traslación de un polígono, en cada caso, se puede considerar que se está formando un cuerpo geométrico. Observa, ¿qué cuerpo geométrico se forma?, ¿por qué?

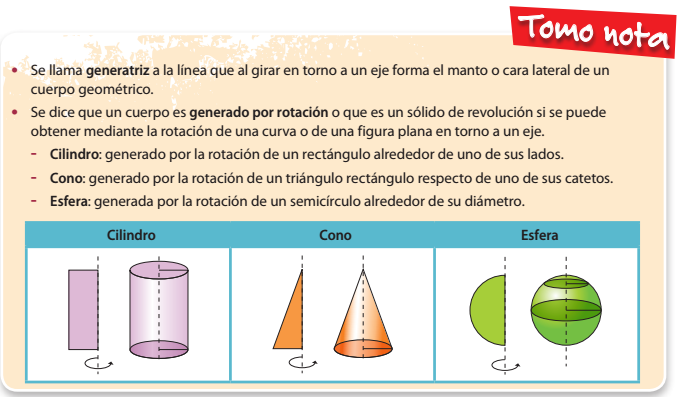
En la imagen, mediante la traslación de un rectángulo se obtiene un
paralelepípedo, y mediante la traslación de un hexágono, un prisma
de base hexagonal. Observa que para que se genere efectivamente
un cuerpo, el vector de traslación no puede ser paralelo al plano que
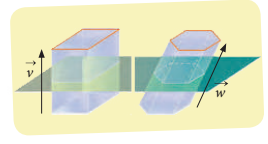
contiene el polígono. — En la imagen, mediante la traslación de un rectángulo se obtiene un paralelepípedo, y mediante la traslación de un hexágono, un prisma de base hexagonal. Observa que para que se genere efectivamente un cuerpo, el vector de traslación no puede ser paralelo al plano que contiene el polígono.

En general, se dice que un cuerpo es generado por traslación si se puede formar mediante la traslación de una figura plana, respecto de un vector no nulo y no paralelo al plano de la figura.

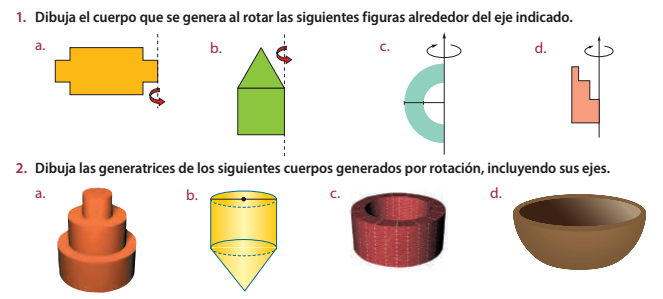
Actividad Lección 1

Resuelve los siguientes ejercicios

De los cuerpos geométricos que conoces, ¿cuáles se pueden generar mediante traslaciones?, ¿qué tipo de traslaciones?

Supón que un cuadrado tiene uno de sus vértices en el origen, con uno de sus lados sobre el eje X y el otro sobre el eje Y y cuyo lado mide 4 unidades de longitud. a. ¿Qué cuerpo se genera al trasladar este cuadrado por el vector (0, 0, 4)? b. ¿Cuál es el volumen de este cuerpo?, ¿por qué? c. ¿Cuál es el área total del cuerpo generado? Justifica. d. Si el vector de traslación fuera (0, 0, –8), ¿qué cuerpo se generaría y cuál sería su volumen? Explica.

Lección 2: Volumen de un prisma

¿Cómo hacerlo? Calcula el volumen de prisma de la siguiente figura, si su base es un octógono regular.

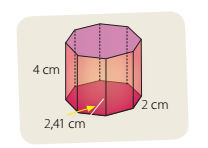
Primero, se calcula el área de la base del prisma (AB). Para esto, se puede
dividir por 2 el producto del perímetro de la base (PB) por la medida del
apotema (ap).
AB = ap · PB
2 = 2,41 · 16
2 = 19,28
Luego, se multiplica el área de la base por la altura, para calcular el volumen (V).
V = 19,28 · 4 = 77,12
Por lo tanto, el volumen del prisma es 77,12 cm3. — Primero, se calcula el área de la base del prisma (AB). Para esto, se puede dividir por 2 el producto del perímetro de la base (PB) por la medida del apotema (ap). AB = ap · PB 2 = 2,41 · 16 2 = 19,28 Luego, se multiplica el área de la base por la altura, para calcular el volumen (V). V = 19,28 · 4 = 77,12 Por lo tanto, el volumen del prisma es 77,12 cm3.

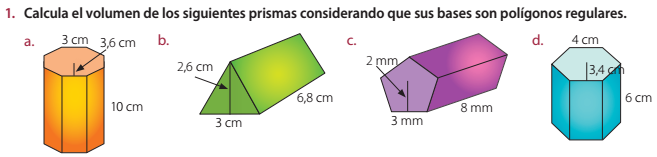
Actividades Lección 2

Resuelve las siguientes actividades:

Uno de los primeros computadores electrónicos medía 15 m de largo, 4 m de ancho y 3 m de alto. Actualmente, un notebook puede medir 30 cm de largo, 20 cm de ancho y 2 cm de alto. ¿Cuántas veces mayor es el volumen del antiguo computador respecto del notebook actual?

Calcula el volumen de un prisma triangular, de altura 6 cm y por base un triángulo equilátero, cuyo lado mide 10 cm. Explica, paso a paso, cómo lo hiciste.

Un prisma de base cuadrada, cuyas dimensiones son 9 cm de arista basal y 15 cm de altura, se corta de tal manera que se obtienen dos prismas idénticos de base triangular. ¿Cuál es el volumen de cada uno de los prismas nuevos?

Lección 3: Volumen de cilindros

Aprenderé a calcular el volumen de cilindros

Observa la siguiente ilustración.

Principio de Cavalieri: si dos cuerpos tienen la misma altura y bases de igual área, y al cortarlos por cualquier plano paralelo a las bases el área de las secciones es la misma, ambos tienen el mismo volumen Como se puede observar en la imagen anterior, los cuerpos tienen igual altura, y si sus secciones planas tienen igual área, se puede aplicar el principio de Cavalieri; por lo tanto, el volumen del cilindro depende de la altura y del área de la base, al igual que en el caso del volumen del prisma, luego se tiene que: Vcilindro = h · B (B: área de la base; h: altura del cilindro) Vcilindro =

Actividades Lección 3

Desarrolla las siguientes actividades:

Calcula el volumen aproximado de cada cilindro a partir de las medidas dadas.

a. Radio: 3 cm, altura: 6 cm b. Diámetro: 4 cm, altura: 5 cm c. Radio: 7 cm, altura: 10,5 cm d. Diámetro: 12 cm, altura: 8 cm e. Radio: 6,5 cm, altura: 10 cm f. Diámetro: 24 cm, altura: 25 cm

Calcula el volumen del cilindro que se genera al girar un rectángulo de 3,5 cm de ancho y 5,8 cm de alto en torno a su altura.

Lección 4: Volumen de pirámides

Aprenderé a: calcular el volumen de una pirámide, recta u oblicua. Comprender la argumentación que justifica la relación entre el volumen de la pirámide y el volumen del prisma.

Volumen de una pirámide

Actividades Lección 4

Resuelve las siguientes actividades

Calcula el volumen de cada pirámide.

a. Base triangular de área 42 cm2 y altura de la pirámide 15 cm. b. Base en forma de triángulo rectángulo, cuyos catetos miden 6 cm y 8 cm, y altura 10 cm. c. Base en forma de triángulo equilátero de lado 6 m y altura de la pirámide 8 m.

La base de una pirámide es un triángulo equilátero de lado 4 cm y de altura 3,5 cm, y su volumen es 21 cm3. ¿Cuál es la altura de la pirámide?

El volumen de una pirámide de base triangular es 96 cm3. Si la base tiene 32 cm2 de área, ¿cuánto mide su altura?

Lección 5: Volumen de Conos

Aprenderé a: Determinar y aplicar la expresión para calcular el volumen de un tronco de cono.

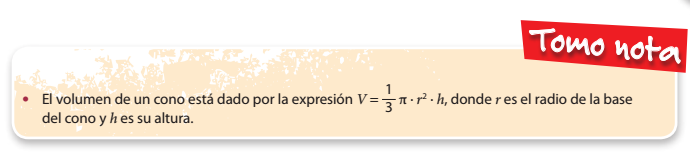
Actividades Lección 5:

Calcula el volumen aproximado de cada cono a partir de las medidas dadas. a. Radio: 9 cm, altura: 12 cm b. Diámetro: 8 cm, altura: 7 cm c. Radio: 12 cm, altura: 15 cm d. Radio: 16 cm, altura: 10 cm e. Generatriz: 26 cm, altura: 24 cm f. Generatriz: 15 cm, radio: 9 cm

La torre de un castillo está formada por un cilindro circular recto de 8 m de diámetro y 16 m de altura, y por un cono de 12 m de altura. Calcula el volumen de la torre.

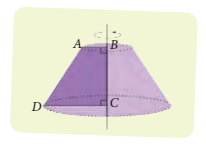
Volumen de un cono truncado

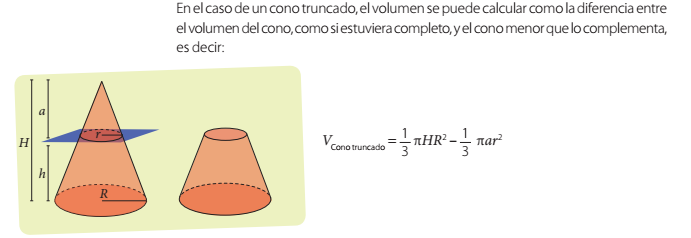
Considera el cono truncado cuyas medidas del radio de la base son 11 cm y 6 cm respectivamente y cuya generatriz mide 13 cm. a. Calcula la altura del cono truncado. b. Calcula el volumen del cono truncado que se genera

Evalúa tus aprendizajes

Resuelve las siguientes preguntas de selección múltiple:

A un cubo de 6 cm de arista se le cortó, desde un vértice, un cubito, de modo que el volumen del cuerpo resultante es de 189 cm3. ¿Cuánto mide la arista del cubito?