Operaciones con vectores.
suma de vectores.
La suma de los vectores podemos realizarla de dos maneras diferentes, analítica y gráficamente.
• Procedimiento Gráfico
Método del paralelogramo
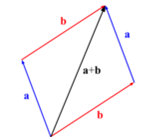Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan, completando el resto del paralelogramo con las paralelas a cada uno . El resultado de la suma se obtiene partiendo del origen de ambos vectores.
El método del paralelogramo es un método gráfico que sirve para sumar sólo dos vectores a la vez. Por lo cual este método es recomendable si se tienen dos vectores. En este método se realiza el siguiente procedimiento:
Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan, completando el resto del paralelogramo con las paralelas a cada uno . El resultado de la suma se obtiene partiendo del origen de ambos vectores.
El método del paralelogramo es un método gráfico que sirve para sumar sólo dos vectores a la vez. Por lo cual este método es recomendable si se tienen dos vectores. En este método se realiza el siguiente procedimiento:- Lo primero que se tiene que hacer es elegir una escala y dibujar a escala los dos vectores a sumar a partir de un origen en común.
- Después se trazan vectores paralelos a los dos vectores a sumar para formar un paralelogramo.
- Enseguida se dibuja el vector resultante (suma de los dos vectores) que va desde el origen en común hasta donde se unen los vectores paralelos (diagonal del paralelogramo).
- Por último se mide la magnitud del vector resultante con una regla (se usa el factor de escala para escribir la magnitud del vector en sus unidades originales) y su dirección con el transportador.
Método del polígono
Consiste en disponer gráficamente un vector a continuación de otro, es decir, el extremo inicial del vector "b" coincide con el extremo final del vector "a". Luego se traza una diagonal que une el inicio del vector "a" con el resto de los extremos.
El método del polígono es otro método gráfico que también sirve para sumar vectores, pero a diferencia del método anterior sirve para sumar dos o más vectores a la vez. Por lo cual este método gráfico es el más usado para sumar vectores gráficamente. En este método se realiza el siguiente procedimiento:
Consiste en disponer gráficamente un vector a continuación de otro, es decir, el extremo inicial del vector "b" coincide con el extremo final del vector "a". Luego se traza una diagonal que une el inicio del vector "a" con el resto de los extremos.
El método del polígono es otro método gráfico que también sirve para sumar vectores, pero a diferencia del método anterior sirve para sumar dos o más vectores a la vez. Por lo cual este método gráfico es el más usado para sumar vectores gráficamente. En este método se realiza el siguiente procedimiento:- Lo primero que se tiene que hacer es elegir una escala apropiada para trazar los vectores.
- Después se dibujan estos vectores a sumar uno enseguida del otro, es decir, se traza el primer vector y al final de este se comienza a trazar el segundo vector y así sucesivamente con todos los vectores a sumar, manteniendo siempre su magnitud y dirección.
- Enseguida se dibuja el vector resultante (suma de los vectores) que va desde el origen hasta el final del último vector.
- Por último se mide la magnitud del vector resultante con una regla (se usa el factor de escala para escribir la magnitud del vector en sus unidades originales) y su dirección con el transportador.
• Procedimiento analítico o algebraico
• Suma de Vectores Unitarios
Frecuentemente las cantidades vectoriales se expresan en términos de 
unitarios. Un vector unitario es un vector sin dimensiones que tiene magnitud igual a uno. Sirven para especificar una dirección determinada. Se usan los símbolos i, j y k para representar vectores unitarios que apuntan en las direcciones x, y y z positivas, respectivamente.Ahora V puede escribirse
V = Ax i + Ay j
Si necesitamos sumar el vector A = Ax i + Ay j con el vector
B = Bx i + By j escribimos
R = A + B = Ax i + Ay j + Bx i + By j = (Ax + Bx)i + (Ay + By)j
Las componentes de R (=A + B) son Rx = Ax + Bx y Ry = Ay + By
unitarios. Un vector unitario es un vector sin dimensiones que tiene magnitud igual a uno. Sirven para especificar una dirección determinada. Se usan los símbolos i, j y k para representar vectores unitarios que apuntan en las direcciones x, y y z positivas, respectivamente.Ahora V puede escribirse
V = Ax i + Ay j
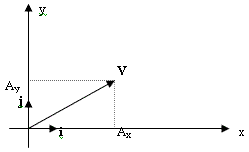Si necesitamos sumar el vector A = Ax i + Ay j con el vector
B = Bx i + By j escribimos
R = A + B = Ax i + Ay j + Bx i + By j = (Ax + Bx)i + (Ay + By)j
Las componentes de R (=A + B) son Rx = Ax + Bx y Ry = Ay + ByResta de vectores
Observaciones:
1. Dado un vector a, su opuesto - a tiene el mismo módulo, la misma dirección y sentido contrario al de a, Basta con ver la construcción de - a.
2. Dados dos vectores a y b, existe un único vector x que verifica a = x + b.
Si existe tal vector, sería: a = b + x → (- b) + a = (- b) + ( b + x)Por la propiedad asociativa, (- b) + ( b + x) = [ (- b) + b] + x = 0 + x = x
Así, el único vector que puede verificar tal propiedad es el vector
x = (- b) + a.
Falta ver que efectivamente la verifica: b + x = b + [ (- b) + a] = [b + (- b)] + a = 0 + a = a, que es la igualdad buscada.
El vector (-b) + a recibe el nombre de diferencia entre los vectores a y b, y suele representarse por a - b.
Para restar dos vectores libres 
y 
se suma con el opuesto de .Las componentes del vector resta se obtienen restando las componentes de los vectores.
Ejemplo:
y se suma con el opuesto de .Las componentes del vector resta se obtienen restando las componentes de los vectores.
Ejemplo: