IIC-RETTA DI EULERO
Retta di Eulero
La retta di Eulero è una retta che passa per baricentro1, ortocentro2 e circocentro3 di ogni triangolo ed esiste un teorema che può verificarlo.
Solamente nei triangoli equilateri questi punti notevoli coincidono e quindi esistono infinite rette che passano per essi.
1 Il baricentro: è il punto d'intersezione delle mediane, i segmenti che congiungono i vertici ai punti medi degli angoli opposti.
2 L'ortocentro: è il punto d'intersezione delle tre altezze del triangolo.
3 Il circocentro: è il punto d'intersezione degli assi di ogni lato, cioè le rette perpendicolari ai lati che passano per il loro punto medio.
altro sui punti notevoli: https://www.geogebra.org/m/q9gnrkd3 di Giuseppe Romano
Costruzione
Costruzione (triangolo equilatero)
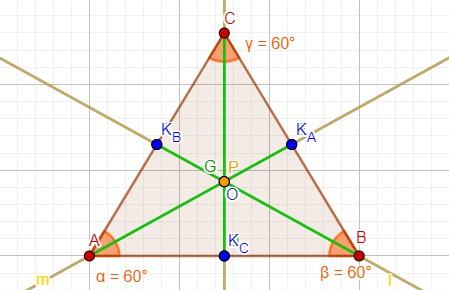
IL TEOREMA
Teorema della retta di Eulero
Il teorema della retta di Eulero dimostra che i tre punti notevoli che abbiamo visto prima sono allineati e mostra la proporzione tra il segmento dal baricentro all'ortocentro e quello dal circocentro al baricentro.
IPOTESI:
| | | | | | | | | TESI:
|
Costruzione
Dimostrazione
Consideriamo lo stesso triangolo scaleno ABC che abbiamo visto prima. Costruiamo il triangolo mediano DEF (i cui vertici sono i punti medi dei lati del triangolo ABC) che, come conseguenza del teorema di Talete, è simile ad ABC ma in rapporto 1 a 2. Poi consideriamo i triangoli GOC e DGP.
- Per dimostrare che G, O e P sono allineati dobbiamo considerare gli angoli PGD e CGO che sono congruenti perché opposti al vertice e di conseguenza sono congruenti anche gli PGC e DGO: possiamo quindi dire che PGC+CGO = PGD+DGO = 180° e che l'angolo PGO è piatto. Come volevasi dimostrare P, G e O sono allineati.
- Adesso ci rimane da dimostrare che il lato GO del triangolo GOC è il doppio del lato PG del triangolo DPG. Dobbiamo dimostrare che i due triangoli che hanno il vertice G sono simili e possiamo farlo attraverso il primo criterio di similitudine dei triangoli (angoli ordinatamente congruenti) dimostrando che gli angoli in G sono congruenti perché opposti al vertice e gli angoli PDC e GCO sono congruenti perché angoli alterni interni delle rette parelle, costituite dall'altezza di C e dall'asse passante per D, tagliate dalla trasversale e mediana CD. I due angoli restanti sono congruenti. Poi come indiretta conseguenza del teorema di Talete conosciamo il teorema del baricentro del triangolo che dimostra che il baricentro nei triangoli divide ogni mediana in due parti e quella che contiene il vertice è il doppio dell'altra, perciò CG è uguale al doppio di GD e quindi il rapporto tra i due triangoli simili è di 2 a 1: per questo anche i lati PG e GO sono in proporzione. É quindi dimostrato che GO = 2PG
![[size=150]La proporzione è ancora più evidente nel triangolo rettangolo (con angolo retto in B per esempio) in cui l'[color=#0000ff][b]altezza di C[/b][/color] coincide con il lato CO e l'[color=#f1c232][b]altezza di D[/b][/color] del triangolo mediano coincide con FD. Il rapporto è [b]2 a 1[/b] per le caratteristiche del triangolo mediano viste prima e perciò una volta dimostrata la somiglianza dei due triangoli si poteva confermare la tesi.[/size]](https://www.geogebra.org/resource/rj9f7fkz/CU5EA73rg1wcGqRs/material-rj9f7fkz.png)
Francesco Giannandrea - 09/03/2021
Prof.ssa Marisa Montanarelli