オイラーの発想

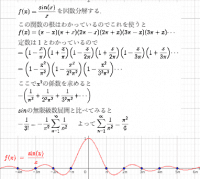
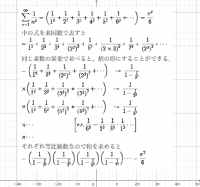
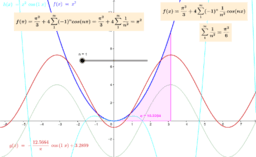
無限級数の和をオイラーの発想を手掛かりに考えてみます。数学ではよく対象とするものを別のモノに置き換えます。ここでは関数を冪級数に置き換えるのです。オイラーはこうやって無限級数の和を自在な発想で求めていっています。そしてバーゼル問題をこの考えで解くのです。この発想が実に楽しいのです。一応参考文献をあげておきます。「三角関数の展開」 https://hamaguri.sakura.ne.jp/sankakukansu.pdf 「 ベキ級数からオイラーの公式まで ・・・テーラー展開、マクローリン展開、そしてオイラーの公式」 https://www.geogebra.org/m/UvjCe3G9 素数と円周率πが見事に結びつく不思議を味わってみましょう。このような不思議が見つかると、この級数を拡張したくなります。それが、ゼータ関数です。