AR Bottle (ATM Workshop)
Mapping onto the National Curriculum in England:
Key Stage 5
Overarching Theme 3 - Mathematical Modelling (applies to both Mathematics and Further Mathematics curricula)
- OT3.1 [Translate a situation in context into a mathematical model, making simplifying assumptions].
- OT3.2 [Use a mathematical model with suitable inputs to engage with and explore situations (for a given model or a model constructed or selected by the student)].
- OT3.3 [Interpret the outputs of a mathematical model in the context of the original situation (for a given model or a model constructed or selected by the student)].
- OT3.4 [Understand that a mathematical model can be refined by considering its outputs and simplifying assumptions; evaluate whether the model is appropriate].
- OT3.5 [Understand and use modelling assumptions].
- Hyperbolic functions - criteria H1 and H2 as defined in Section H: "Understand the definitions of hyperbolic functions...tanh x, including...domains and ranges, and be able to sketch their graphs"; "...integrate hyperbolic functions".
- Volumes of revolution - criterion E2 as defined in Section E: "Derive formulae for and calculate volumes of revolution".
Instructions
1. Find a bottle-shaped object and place it on a flat, matt surface in front of you (such as a wooden table), laying on its side (otherwise the GeoGebra AR's x-y plane will not appear horizontal, which its functionality needs).
2. Open the 3D calculator on your smartphone or tablet's GeoGebra app. You can find and open this activity in the app by searching for the following code: dzf8qwnu.
3. Use your finger or thumb to orientate the blue bottle already given on your screen so that it appears to be facing in the same direction the bottle you wish to model.
4. Enable AR by clicking the circle with "AR" written inside it - to the bottom-left of the image on screen. Now try to overlay the real bottle with the virtual blue bottle, by clicking on an origin point roughly in the same part (near the centre of the start of the real bottle's neck) as viewed through the device's screen. This should fix the axes in place there.
5. You now can pinch together your finger and thumb as they make contact with the screen - or move them apart - to alter the scale of the virtual blue bottle.
6. Once you have a rough match, experiment with the three sliders 
labelled "top", "bottom" and "curve" to finesse the model until you have matched the real bottle's shape as best as you can.
7. Scroll down in the "Algebra" view until you find the large blue bullet point on the left of the definition for "c(u,v)". By clicking on the three vertical dots to the right of this definition, and selecting "Settings" at the bottom of the menu that then appears, you can change both the colour and opacity of your virtual bottle to best match the real one.
8. Take a screenshot (if you wish to keep evidence of your creation). Walk around to change your viewing aspect and take more screenshots.
9. How can you use both paper and pencil/pen and GeoGebra to calculate the volume of the bottle? How might you verify your answer experimentally?
10. Now consider the affordances and limitations of this modelling system in terms of:
a) its other potential applications;
b) the mathematics involved (you will find this information within the "Algebra" entries and you may need to use your finger or thumb to swipe a line of algebraic code to the left or right to read it in full).
labelled "top", "bottom" and "curve" to finesse the model until you have matched the real bottle's shape as best as you can.
7. Scroll down in the "Algebra" view until you find the large blue bullet point on the left of the definition for "c(u,v)". By clicking on the three vertical dots to the right of this definition, and selecting "Settings" at the bottom of the menu that then appears, you can change both the colour and opacity of your virtual bottle to best match the real one.
8. Take a screenshot (if you wish to keep evidence of your creation). Walk around to change your viewing aspect and take more screenshots.
9. How can you use both paper and pencil/pen and GeoGebra to calculate the volume of the bottle? How might you verify your answer experimentally?
10. Now consider the affordances and limitations of this modelling system in terms of:
a) its other potential applications;
b) the mathematics involved (you will find this information within the "Algebra" entries and you may need to use your finger or thumb to swipe a line of algebraic code to the left or right to read it in full).How to Construct your own Bottle Modeller
Construction of this applet requires a knowledge of both:
- A range of appropriate Cartesian functions to choose from of the form y = A f(b (x - a)) + c, with a knowledge of the effect on the curve of altering each of the variables A, a, b and c. The hyperbolic tangent function (tanh(x)) was chosen by the author but this is by no means the best fit for all types of bottle.
- The syntax of GeoGebra Computer Algebra System coding - including defining: variables using sliders; a function of those variables; a surface of revolution related to both of these.
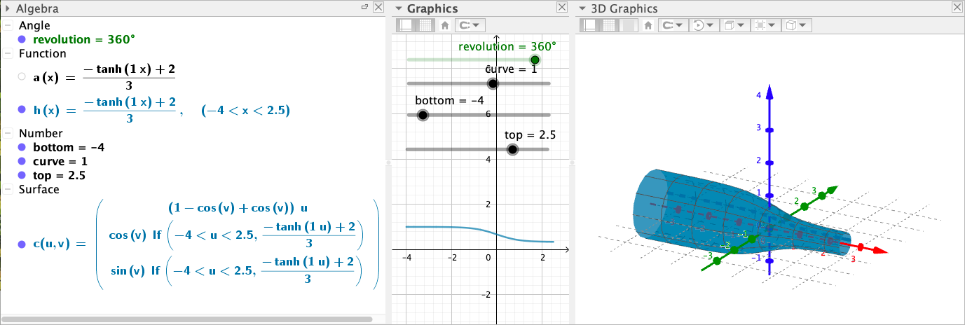
Input Code, 2D Curve Segment (with Sliders) and 3D Rendering of Revolution around x-Axis
Video Demo of Visual Optimisation
Volume and Surface of Revolution
1. Using an appropriate integral substitution and a hyperbolic trigonometric identity relating hyperbolic tangents to hyperbolic secants, calculate:
a)
b)
2. In the above model, the function was used to match the blue bottle's shape.
a) Half of a Christmas cracker is modelled using the simpler function , within the domain . What is the cracker's volume?
b) What is the domain of values within which the curve for was plotted?
c) The label on the bottle says it contains 1 litre of water. Now determine the volume of revolution of and use the scale shown on the video screenshot above to deduce how much more water this bottle could contain if filled to the brim. (Assume the base is flat.)
3. (Warning: difficult!) Estimate how much blue plastic would be needed if a 2mm thick sheet of it had been moulded to manufacture this bottle. (Assume the base is flat.)