Ángulos que difieren 180º
Ángulos que difieren 180º
Dos ángulos difieren 180º cuando la diferencia entre ellos es de 180 º:
Si dos ángulos difieren 180º, podemos establecer ciertas relaciones entre las rezones trigonométricas de dichos ángulos.
Utiliza la siguiente construcción de Geogebra para conocer cuáles son esas relaciones
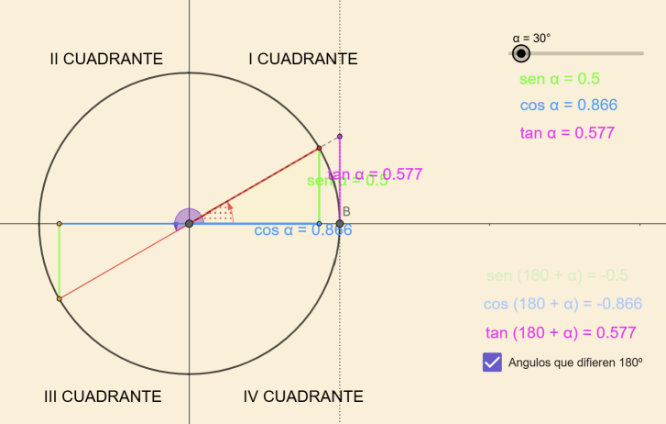
Relación entre ángulos que difieren 180º
Ejemplo:
Sabiendo que sen 30º = 0,5, calcula sen 210º.
Respuesta: sen 210º vale -0,5, según la siguiente construcción.
Ahora, realiza estas dos actividades:
Sabiendo que sen 35º = 0,574, cos 35º = 0,819 y tg 35º = 0,7, calcula las razones trigonométricas de un ángulo de 215º. Sabiendo que 75º = 0,966, cos 75º = 0,259 y tg 75º = 3,732, calcula las razones trigonométricas de un ángulo de 255º. Utiliza la construcción de Geogebra para comprobar tus resultados y adjunta enlaces a capturas de pantalla donde se muestre dicha construcción.
¿Cómo debe ser la solución?
Debes contestar con el valor de las razones trigonométricas y con el enlace de la captura de pantalla:
Si la pregunta es: sabiendo que sen 44º = 0,695, calcula sen 224º
Tendrías que responder:
sen 224º = -0,695 (ángulos que difieren 180º)
y adjuntar una imagen de este estilo: IMAGEN