"Thales-Kreis" für Kreisbüschel
Wo schneiden sich die Geraden aus 2 Geradenbüscheln unter einem rechten Winkel?
Antwort: Die Geraden aus 2 Geradenbüschel schneiden sich auf dem THALES-Kreis rechtwinklig.
Im Applet unten wird der THALES-Kreis als Ortskurve nach der angegebenen Bedingung erzeugt:
die Geraden des einen Büschels werden durch einen Punkt auf einem konzentrischen Kreis um den
Büschelpunkt bewegt!
Spiegelt man den anderen Büschelpunkt an der bewegten Geraden, so ist die Verbindungsgerade
orthogonal dazu und schneidet in einem Punkt der gesuchten Ortskurve.
Die Frage: Wo berühren sich die Geraden zweier Geradenbüschel? - erscheint zunächst unsinnig!
Euklidisch schneiden sich zwei Geraden oder sie sind parallel.
Möbiusgeometrisch jedoch berühren zwei parallele Geraden sich in .
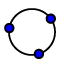
Wo schneiden sich die Kreise zweier elliptischen Kreisbüschel unter einem rechten Winkel?
Wo berühren sich die Kreise zweier elliptischen Kreisbüschel?
Antwort: In beiden Fällen sind die Ortskurven bizirkulare Quartiken, die möbiusgeometrisch Transformierte
von CASSINI-Kurven sind!
Ein elliptisches Kreisbüschel besteht aus allen Kreisen durch die zwei Grundpunkte eines solchen Büschels.
Die ge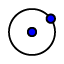
gebra-Konstruktion der Ortskurven ist ähnlich wie die des THALES-Kreises:
Man bewege einen Punkt auf einem zum Kreisbüschel orthogonalen Kreis um die Büschelpunkte und bewege
mit diesem Punkt einen Kreis aus dem Büschel. An diesem Kreis spiegele man die Grundpunkte des anderen Büschels.
-Verbunden erhält man einen orthogonalen Kreis aus dem 2. Büschel; bzw. etwas komplizierter einen Berührkreis.
Die Kreise sind nicht immer reell!
Übrigens: Der Berührort ist auch der Ort, in welchem sich die elliptischen Kreise des einen Büschels
und die hyperbolischen Kreise des anderen Büschels orthogonal schneiden!
Die hyperbolischen Kreise eines Büschels sind die orthogonalen Kreise zu den elliptischen Kreisen eines Büschels.
gebra-Konstruktion der Ortskurven ist ähnlich wie die des THALES-Kreises:
Man bewege einen Punkt auf einem zum Kreisbüschel orthogonalen Kreis um die Büschelpunkte und bewege
mit diesem Punkt einen Kreis aus dem Büschel. An diesem Kreis spiegele man die Grundpunkte des anderen Büschels.
-Verbunden erhält man einen orthogonalen Kreis aus dem 2. Büschel; bzw. etwas komplizierter einen Berührkreis.
Die Kreise sind nicht immer reell!
Übrigens: Der Berührort ist auch der Ort, in welchem sich die elliptischen Kreise des einen Büschels
und die hyperbolischen Kreise des anderen Büschels orthogonal schneiden!
Die hyperbolischen Kreise eines Büschels sind die orthogonalen Kreise zu den elliptischen Kreisen eines Büschels.
THALES-Kreis
CASSINI-Kurven?
Dass es sich bei dem Ort, auf welchem sich die Kreise zweier Kreisbüschel berühren, oder unter 90°
oder allgemeiner unter konstantem Winkel schneiden, um bizirkulare Quartiken handelt, läßt sich
mit nicht zu großem Aufwand begründen.
Größere Schwierigkeiten bereitet es nachzuweisen, dass es sich speziell um
möbiustransformierte CASSINI-Kurven handelt.
Auf den Seiten
haben wir die CASSINI-Eigenschaft untersucht für den Fall, dass die 4 verschiedenen Grundpunkte in Normalform liegen.
Normalform bedeutet, dass die 4 Grundpunkte in Paaren punktsymmetrisch zu den 6 Punkten einer ON-Basis liegen,
das sind die Schnittpunkte von 3 paarweise orthogonalen Kreisen: beispielsweise die Punkte
als Schnittpunkte der Achsen und des Einheitskreises. In Normalform liegen dann die Punkte mit .
Es ist also zu zeigen, dass zu 4 verschiedenen Punkten stets eine ON-Basis existiert, bezüglich
der die Punkte in Normalform liegen.
Geometrisch: Die Konstruktion ist ziemlich aufwändig und wird in 3 fast identischen Schritten durchgeführt.
4 verschiedene Punkte können auf 3 verschiedenen Weisen in 2 Punktepaare zerlegt werden.
Für ein solches Punktepaar bestimme man zuerst die 2 Kreise des Kreisbüschels durch die beiden
anderen Punkte und dazu die winkelhalbierenden Kreise. Dies gelingt auch, wenn die 4 Punkte konzyklisch sind!
Entsprechend verfährt man für das andere Punktepaar. Es ergeben sich 4 winkelhalbierende Kreise.
2 von diesen Kreisen sind hyperbolische Kreise (sie schneiden sich nicht oder sind identisch), die 2 anderen sind
elliptische Kreise für dasselbe Büschel. Die Schnittpunkte dieser Kreise sind 2 Punkte der gesuchten ON-Basis.
Die beiden Punkte-Paare liegen harmonisch zu diesen Schnittpunkten.
Für die beiden anderen Aufteilungen in Punkte-Paare erhält man 2*2 weitere Punkte der ON-Basis.
Entscheidend ist: diese 6 Punkte sind die Schnittpunkte von 3 paarweise orthogonalen Kreisen.
| CASSINI, Wurzel und Umfangswinkel | CASSINI-Peripheriewinkel 1 |
| CASSINI, Wurzel und Umfangswinkel -2- | CASSINI-Peripheriewinkel 2 |
Algebraisch: Die Berechnung der ON-Basis wird ganz einfach und kurz, wenn man sie in der LIE-Algebra der
Möbiusgruppe durchführt!
Die LIE-Algebra der Möbiusgruppe ist ein komplexer 3-dimensionaler Vektorraum mit
nicht-ausgearteter symmetrischer Bilinearform und einem Kreuzprodukt - dem LIE-Produkt [ , ].
Man kann die LIE-Algebra als Komplexifizierung des euklidischen Vektorraumes auffassen, die quadratische
Form ist allerdings nicht positiv definit - daher eignet sich die Bezeichnung "Skalarprodukt" nicht so sehr.
Kreisbüschel und ihre Loxodrome mit den Grundpunkten lassen sich mit den Vektoren aus
und deren komplexen Vielfachen identifizieren.
Zu 4 verschiedenen Punkten lassen sich die Kreisbüschel-Paare {}, {}
und {} bilden. Die Vektoren , und repräsentieren
3 Kreisbüschel, deren Grundpunkte eine ON-Basis bilden.
Das ergibt sich aus einer einfachen Rechnung: die Vektoren sind paarweise orthogonal bezüglich und
sie sind orthogonal zu ihren Faktoren: woraus insbesondere folgt, dass die Grundpunkte der Faktoren harmonisch
zu den Grundpunkten der zugehörigen ON-Basis-Vektoren liegen.
Exemplarisch: es gilt ; woraus folgt, dass und harmonisch zu den
Grundpunkten von liegen.
Wählt man die ON-Basis so dass die Grundpunkte von sind,
so gilt bezüglich dieser ON-Basis die Punktsymmetrie .
Die LIE-Produkt-Berechnungen sind eine Folge der Entwicklungs-Regeln für das Kreuzprodukt bzw. für das LIE-Produkt.
Detailliert durchgeführt werden diese Rechnungen in der Aktivität Lage von 4 Punkten
im geogebra-book Moebiusebene.