自由落体运动
一、什么是自由落体运动
当物体在只受重力作用时由静止开始下落的运动被称为自由落体运动。
自由落体要满足两个特征,只受重力作用和无初速释放。
我们周边总有空气,物体下落总会受到空气阻力,理想的自由落体运动只有在真空环境中才存在。
在现实生活中,静止下落时受空气阻力远小于重力的物体可以近似看成自由落体。
比如一棵苹果树上掉下的苹果和树叶,苹果可以看成自由落体,树叶则不行,因为相较于所受的重力,树叶本身受到的空气阻力和浮力更大,完全不可忽略。
跳伞运动员还没打开伞时可以近似看成自由落体,已经打开伞后则不行。

二、伽利略对自由落体运动的研究
自由落体运动在物理学中占据的特殊地位很大程度源于伽利略对它的研究。
古希腊哲学家亚里士多德基于观察提出了这样一个观点:物体从高空中下落的速度与重量成正比。比如苹果和树叶从同样的高度下落,苹果很快落地,树叶则慢慢悠悠地在空中飘荡。
伽利略用了一个思想实验来反驳亚里士多德的观点:
假设有一个大球,质量为,有一个小球,质量为。根据亚里士多德的观点,大球和小球从同一高度掉下,大球会先落地;
假设大球落地时速度为,小球落地时速度为。
现在将两个球绑在一起,自由释放。大球下落快,会被下落慢的小球拖着而减慢;小球下落慢,则会被下落快的大球拖着而加快。最后两者的速度应该介于两个球单独释放时的速度的中间,即>>
但是我们根据亚里士多德的观点,两个球绑在一起更重了,应该会比大球单独下落时更快,速度>>。
这就出现了悖论,说明不同重量的物体下落的速度应该一样快。
点击观看真空下落的视频

紧接着,伽利略猜想,物体下落的运动是一个速度随着时间均匀变大的运动,即匀变速直线运动,并设计实验进行了验证。
伽利略时代没有精确计时工具,更没有频闪照片,物体自由下落的时间太快了,来不及反应。于是伽利略将不同的铜球放在一个倾角很小的斜面上让球自由滚下,测量小球等时间间隔的位移。
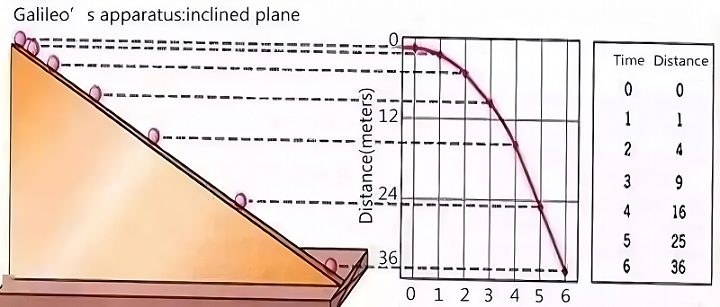
我们现在已经知道了,如果物体做初速度为零的匀变速直线运动,它的位移和运动时间将成正比,即,其时间位移比会满足1:4:9:16……这样的平方比。
伽利略测得不同质量的小球沿同一斜面滚下的等时间位移是一样的,说明小球在斜面上的运动与物体重量无关。
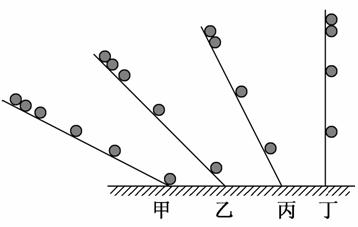
伽利略又增大斜面角度,再测了几组小球的运动,发现虽然单位时间内的位移不一样,但是等时间间隔位移比都满足一样的比例,说明小球从斜面静止滚下的运动无论倾角多少都是匀变速直线运动。
伽利略将这个结论合理外推,假设斜面倾斜角为90°,小球再从斜面滚下就是自由落体了,自由落体运动也应该是匀变速直线运动。
我们现在已经知道了,如果物体做初速度为零的匀变速直线运动,它的位移和运动时间将成正比,即,其时间位移比会满足1:4:9:16……这样的平方比。
伽利略测得不同质量的小球沿同一斜面滚下的等时间位移是一样的,说明小球在斜面上的运动与物体重量无关。
伽利略又增大斜面角度,再测了几组小球的运动,发现虽然单位时间内的位移不一样,但是等时间间隔位移比都满足一样的比例,说明小球从斜面静止滚下的运动无论倾角多少都是匀变速直线运动。
伽利略将这个结论合理外推,假设斜面倾斜角为90°,小球再从斜面滚下就是自由落体了,自由落体运动也应该是匀变速直线运动。
 经过精彩的推理、实验、测量和分析后,伽利略得出了结论:自由落体的物体做的是匀变速直线运动,且这个运动的加速度与物体本身的质量无关。
伽利略对自由落体的研究是物理学结合推理、实验和数学对自然现象进行研究的典范,为后世物理学的发展奠定了坚实的思想基础。
经过精彩的推理、实验、测量和分析后,伽利略得出了结论:自由落体的物体做的是匀变速直线运动,且这个运动的加速度与物体本身的质量无关。
伽利略对自由落体的研究是物理学结合推理、实验和数学对自然现象进行研究的典范,为后世物理学的发展奠定了坚实的思想基础。

我们现在已经知道了,如果物体做初速度为零的匀变速直线运动,它的位移和运动时间将成正比,即,其时间位移比会满足1:4:9:16……这样的平方比。
伽利略测得不同质量的小球沿同一斜面滚下的等时间位移是一样的,说明小球在斜面上的运动与物体重量无关。
伽利略又增大斜面角度,再测了几组小球的运动,发现虽然单位时间内的位移不一样,但是等时间间隔位移比都满足一样的比例,说明小球从斜面静止滚下的运动无论倾角多少都是匀变速直线运动。
伽利略将这个结论合理外推,假设斜面倾斜角为90°,小球再从斜面滚下就是自由落体了,自由落体运动也应该是匀变速直线运动。
我们现在已经知道了,如果物体做初速度为零的匀变速直线运动,它的位移和运动时间将成正比,即,其时间位移比会满足1:4:9:16……这样的平方比。
伽利略测得不同质量的小球沿同一斜面滚下的等时间位移是一样的,说明小球在斜面上的运动与物体重量无关。
伽利略又增大斜面角度,再测了几组小球的运动,发现虽然单位时间内的位移不一样,但是等时间间隔位移比都满足一样的比例,说明小球从斜面静止滚下的运动无论倾角多少都是匀变速直线运动。
伽利略将这个结论合理外推,假设斜面倾斜角为90°,小球再从斜面滚下就是自由落体了,自由落体运动也应该是匀变速直线运动。
 经过精彩的推理、实验、测量和分析后,伽利略得出了结论:自由落体的物体做的是匀变速直线运动,且这个运动的加速度与物体本身的质量无关。
伽利略对自由落体的研究是物理学结合推理、实验和数学对自然现象进行研究的典范,为后世物理学的发展奠定了坚实的思想基础。
经过精彩的推理、实验、测量和分析后,伽利略得出了结论:自由落体的物体做的是匀变速直线运动,且这个运动的加速度与物体本身的质量无关。
伽利略对自由落体的研究是物理学结合推理、实验和数学对自然现象进行研究的典范,为后世物理学的发展奠定了坚实的思想基础。借助现代的测量手段,我们测出伽利略所说的物体做自由落体运动时与物体无关的那个加速度的值是
这个加速度和物体的质量无关,会受到物体所处的纬度、海拔的轻微影响。但只要在地球上,这个值就是几乎不变的,我们把这个值记为,称为重力加速度。
不过在不同星球上重力加速度一般会不一样,比如月球上的重力加速度只有大约,比地球上小得多。
(注:后续为了计算方便我们取)
三、自由落体运动的基本规律
自由落体运动实际上是一种初速度为零,且加速度固定不变的特殊匀变速直线运动,它的运动规律仍满足一般的匀变速直线运动规律,但是更简单。
因为自由落体运动是竖直方向上的运动,我们用来代表位移,再将加速度换成,并让。
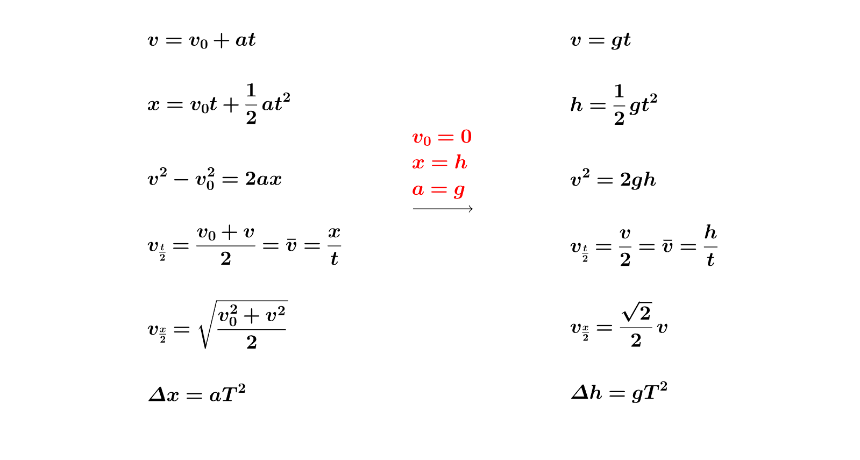
和普通的匀变速直线运动相比,自由落体运动因为已经知道了初速度和加速度,只有末速度、时间、位移三个变量,所以它具有知一求二的特点,即知道任意一个变量就能求出另外两个变量。
再具体点说,、、这三个关系都是一一对应的,我们可以做到知道一个就马上算出另外一个。
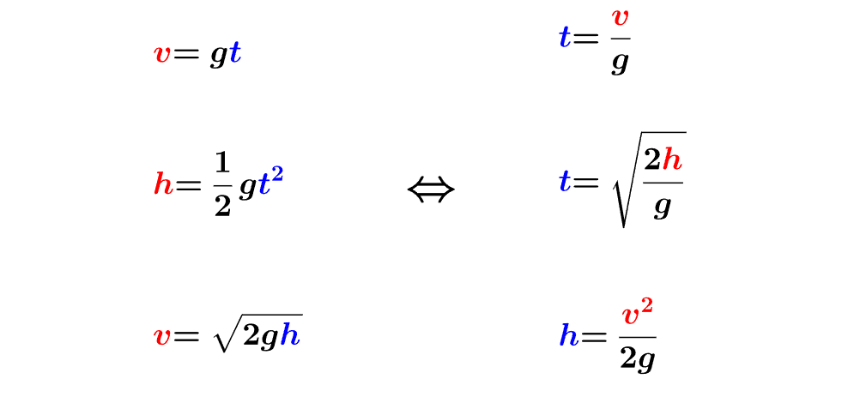
例1:(多选)物体做自由落体运动,取 ,该物体( )
,该物体( )
解析:
前2s内的位移:
第2s末的速度:
前2s平均速度:
故选A、B。
例2:(多选)一个做自由落体运动的物体,其落地速度为20m/s,重力加速度g取10m/s2,则下列描述正确的是( )
A.下落的时间为2s B.下落时距地面的高度为25m
C.下落过程中的平均速度为5m/s D.在下落中点位置的速度为15m/s
解析:
下落时间
下落高度
下落平均速度
中间位置的速度
故选A
例3:(多选)甲、乙两物体分别从10m和20m高处同时自由落下,不计空气阻力,下面描述正确的是( )
A.落地时甲的速度是乙的
B.落地的时间乙是甲的倍
C.下落1s时甲的速度与乙的相同
D.乙的加速度是甲的2倍
解析:
A错、B对。
对自由落体运动来说,无论物体轻重,加速度都是,D错误。
由,两个物体下落时间相同,速度一定相同,C对
| A.在前2s内下落的距离为20m | B.在前2s内平均速度为10m/s |
| C.第2s末的速度为30m/s | D.第2s末的速度为40m/s |
例4:从离地面高的空中自由落下一个小球,落地前瞬间小球的速度为,取 ,求小球落地前最后内的位移的大小。
解析:
小球落地时间
小球下落的位移
小球在内下落的位移
小球在最后内的位移
,求小球落地前最后内的位移的大小。
解析:
小球落地时间
小球下落的位移
小球在内下落的位移
小球在最后内的位移
例5:(多选)如图所示,一栋三层楼房,每层楼高均为3m,且每层楼墙壁正中间有一个高为1m的窗户。现将一石块从楼顶边缘自由释放,不计空气阻力,以下说法正确的是( )
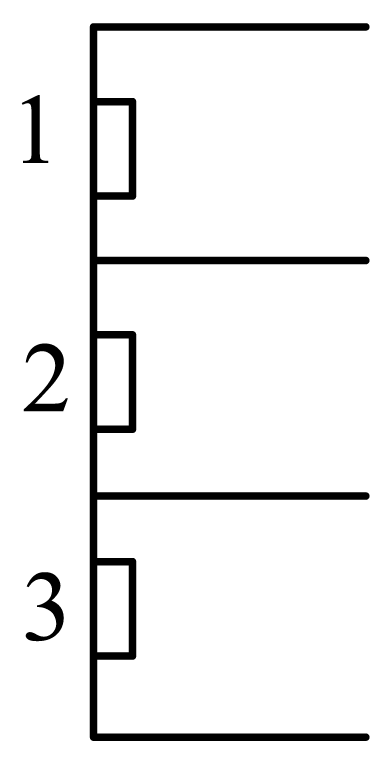 A.石块依次到达三个窗户上边缘的速度大小之比为
B.石块依次通过三个窗户的平均速度之比为
C.石块依次到达三个窗户下边缘的时间之比为
D.石块依次通过三个窗户的时间之比为
解析:
由题意可知,石块经过第一、第二、第三个窗户上边缘时的位移分别为1m、4m、7m,根据可得石块依次到达三个窗户上边缘的速度大小之比,A正确;
根据可得,石块依次经过三个窗户上边缘的时间之比为
石块到达三个窗户下边缘的位移分别为2m、5m、8m,根据可得,石块依次到达三个窗户下边缘的时间之比为,C错误
石块依次通过三个窗户的时间之比为,D正确;
根据可得石块依次通过三个窗户的平均速度之比为,B正确。
故选ABD。
A.石块依次到达三个窗户上边缘的速度大小之比为
B.石块依次通过三个窗户的平均速度之比为
C.石块依次到达三个窗户下边缘的时间之比为
D.石块依次通过三个窗户的时间之比为
解析:
由题意可知,石块经过第一、第二、第三个窗户上边缘时的位移分别为1m、4m、7m,根据可得石块依次到达三个窗户上边缘的速度大小之比,A正确;
根据可得,石块依次经过三个窗户上边缘的时间之比为
石块到达三个窗户下边缘的位移分别为2m、5m、8m,根据可得,石块依次到达三个窗户下边缘的时间之比为,C错误
石块依次通过三个窗户的时间之比为,D正确;
根据可得石块依次通过三个窗户的平均速度之比为,B正确。
故选ABD。
 A.石块依次到达三个窗户上边缘的速度大小之比为
B.石块依次通过三个窗户的平均速度之比为
C.石块依次到达三个窗户下边缘的时间之比为
D.石块依次通过三个窗户的时间之比为
解析:
由题意可知,石块经过第一、第二、第三个窗户上边缘时的位移分别为1m、4m、7m,根据可得石块依次到达三个窗户上边缘的速度大小之比,A正确;
根据可得,石块依次经过三个窗户上边缘的时间之比为
石块到达三个窗户下边缘的位移分别为2m、5m、8m,根据可得,石块依次到达三个窗户下边缘的时间之比为,C错误
石块依次通过三个窗户的时间之比为,D正确;
根据可得石块依次通过三个窗户的平均速度之比为,B正确。
故选ABD。
A.石块依次到达三个窗户上边缘的速度大小之比为
B.石块依次通过三个窗户的平均速度之比为
C.石块依次到达三个窗户下边缘的时间之比为
D.石块依次通过三个窗户的时间之比为
解析:
由题意可知,石块经过第一、第二、第三个窗户上边缘时的位移分别为1m、4m、7m,根据可得石块依次到达三个窗户上边缘的速度大小之比,A正确;
根据可得,石块依次经过三个窗户上边缘的时间之比为
石块到达三个窗户下边缘的位移分别为2m、5m、8m,根据可得,石块依次到达三个窗户下边缘的时间之比为,C错误
石块依次通过三个窗户的时间之比为,D正确;
根据可得石块依次通过三个窗户的平均速度之比为,B正确。
故选ABD。
自由落体运动的初速度为零,所以可以直接运用之前所讲的那几个初速度为零的匀变速直线运动的比例推论。
例6:科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光间隔时间正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g取10 m/s2)( )
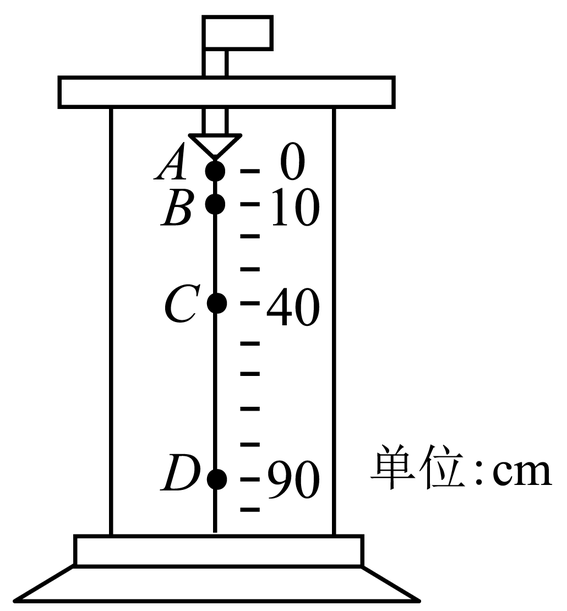
解析:
由图知,,符合初速度为零的等时间位移推论,说明,A错。
我们取AB段位移进行计算,,B对。
,故,C错
由初速度为0的等时间推论,,D错

| A.水滴在下落过程中通过相邻两点之间的时间满足tAB<tBC<tCD |
| B.闪光的间隔时间是 |
| C.水滴在相邻两点间的平均速度满足 |
| D.水滴在各点的速度之比满足vB∶vC∶vD=1∶3∶5 |
例7:屋檐上每隔相同的时间间隔滴下一滴水,当第7滴正欲滴下时,第1滴已刚好到达地面,而第5滴与第4滴分别位于高为1m的窗户的上、下沿,如图所示,问:
(1)滴水的时间间隔是多少;(g取10m/s2)
(2)此屋檐离地面多高。
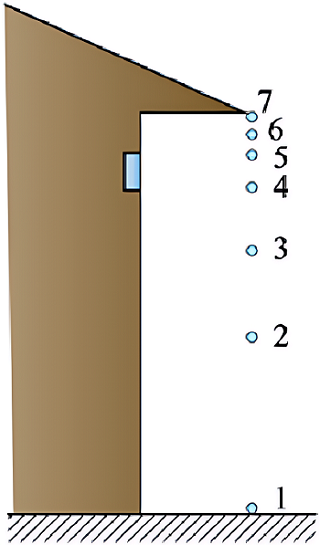 解析:
(1)根据初速度为零的匀加速直线运动的规律可知,
由可知,
根据可得
(2)屋檐离地面高度
解析:
(1)根据初速度为零的匀加速直线运动的规律可知,
由可知,
根据可得
(2)屋檐离地面高度
 解析:
(1)根据初速度为零的匀加速直线运动的规律可知,
由可知,
根据可得
(2)屋檐离地面高度
解析:
(1)根据初速度为零的匀加速直线运动的规律可知,
由可知,
根据可得
(2)屋檐离地面高度自由落体运动的规律和推论只能运用于自由落体运动,初速度一定为0。如果我们选取的是自由落体运动中间的某一段运动,则不属于自由落体运动,是不能硬套自由落体的运动公式的,这时候要当作一般的匀变速直线运动去处理。
例8:(多选)如图是一张在真空实验室里拍摄的羽毛与苹果同时下落的局部频闪照片。已知频闪照相机的频闪周期为T。下列说法正确的是( )
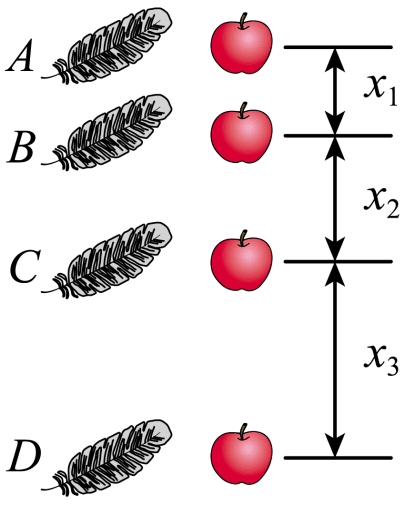
解析:
不知道A点是否为初始释放点,不能直接用初速度为0的等时间推论,A错
同理,C点的速度不能直接用,C错
根据中间时刻速度推论:,B对
根据位移差推论,,D对

| A.x1、x2、x3一定满足 |
| B.羽毛下落到B点的速度大小为 |
| C.苹果在点C的速度大小为2gT |
| D.羽毛下落的加速度大小为 |
四、自由落体运动的几类典型问题
1、先自由落体再减速
例1.跳伞员从的高空自由下落一段距离后才打开降落伞,假设伞打开后以大小为的加速度匀减速下降,到达地面时速度为(g取),求:
(1)跳伞员打开伞时距地面的高度是多少?下落的最大速度为多大?
(2)跳伞员下落的总时间是多少?
解析:
(1)以向下为正方向,
设自由落体的时间为,下落位移,最大速度
打开降落伞后的位移
由题知,
联立上式并代入数据解得:
(2)跳伞员打开降落伞后的减速时间
下落总时间
2、高空坠物避免相撞
例1:如图所示,某居民楼距地面高 阳台上的花盆如受扰动而掉落,掉落过程可看作自由落体运动,花盆可视为质点。一骑手正以
阳台上的花盆如受扰动而掉落,掉落过程可看作自由落体运动,花盆可视为质点。一骑手正以 的速度骑着自行车匀速驶向阳台正下方的通道,自行车长度
的速度骑着自行车匀速驶向阳台正下方的通道,自行车长度 。花盆刚开始掉落时,自行车车头距花盆的水平距离
。花盆刚开始掉落时,自行车车头距花盆的水平距离 ,由于道路狭窄,自行车只能直行通过阳台正下方的通道,且骑手的头部离地面高度
,由于道路狭窄,自行车只能直行通过阳台正下方的通道,且骑手的头部离地面高度 ,为简化计算,设人和车整体高度也为
,为简化计算,设人和车整体高度也为 ,如果花盆下落到这个高度,我们就认为它砸到了车子。求:
,如果花盆下落到这个高度,我们就认为它砸到了车子。求:
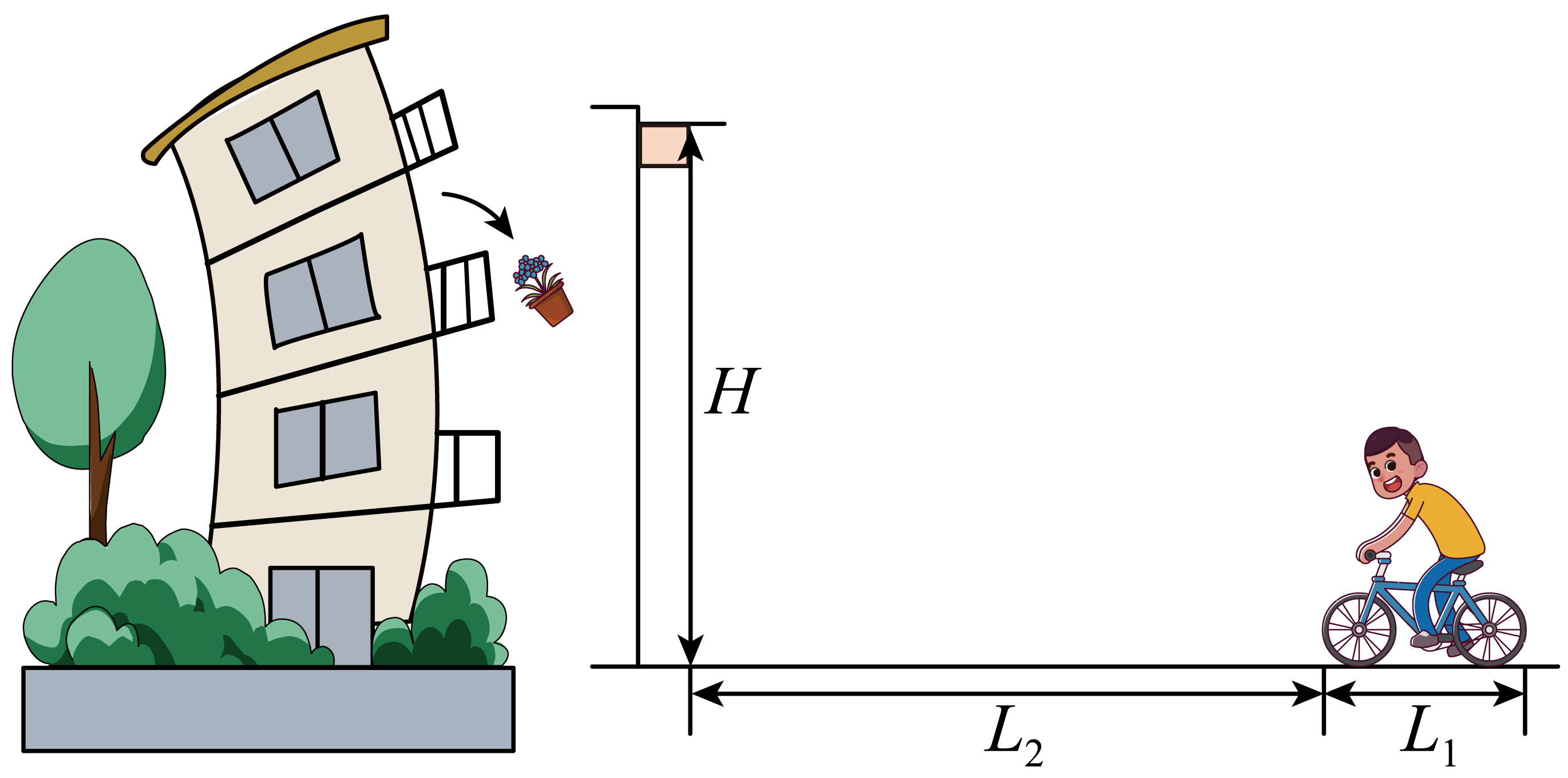 (1)若骑手没有发现花盆掉落,保持匀速直行,通过计算说明自行车是否会被花盆砸到?
(2)若骑手发现花盆开始掉落,且反应时间
(1)若骑手没有发现花盆掉落,保持匀速直行,通过计算说明自行车是否会被花盆砸到?
(2)若骑手发现花盆开始掉落,且反应时间 ,则骑手至少以多大的加速度进行加速,才能确保实现避险。(自行车加速过程可视为匀变速运动)
解析:
(1)花盆掉落至与人头顶等高处的时间为
这段时间内人的位移
因为<<,所以会被砸到。
(2)设骑手加速通过的加速度为,骑手要不被砸,加速通行的位移要满足:
联立解得,
,则骑手至少以多大的加速度进行加速,才能确保实现避险。(自行车加速过程可视为匀变速运动)
解析:
(1)花盆掉落至与人头顶等高处的时间为
这段时间内人的位移
因为<<,所以会被砸到。
(2)设骑手加速通过的加速度为,骑手要不被砸,加速通行的位移要满足:
联立解得,
 (1)若骑手没有发现花盆掉落,保持匀速直行,通过计算说明自行车是否会被花盆砸到?
(2)若骑手发现花盆开始掉落,且反应时间
(1)若骑手没有发现花盆掉落,保持匀速直行,通过计算说明自行车是否会被花盆砸到?
(2)若骑手发现花盆开始掉落,且反应时间3、质点穿过一段距离
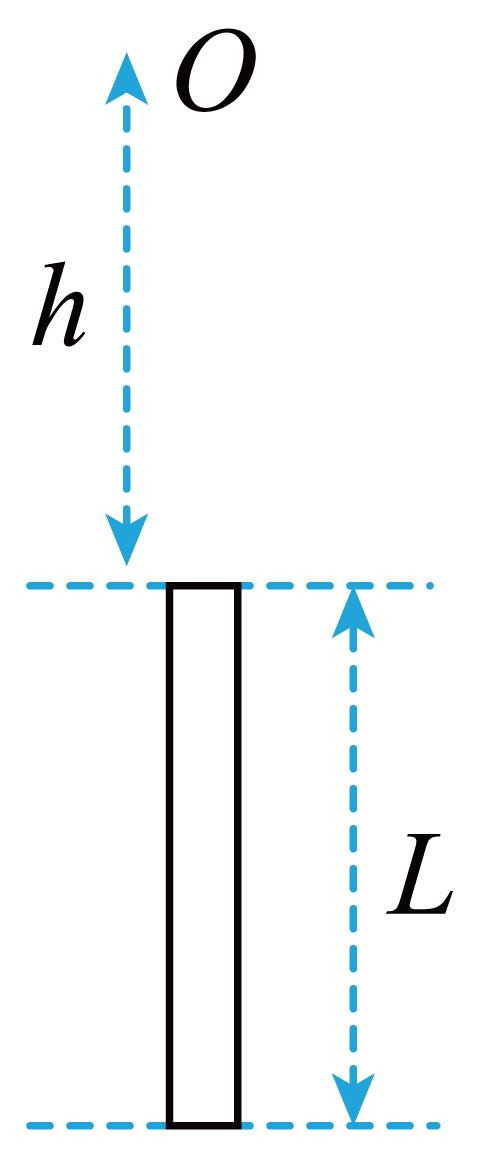
例1:如图所示,一长为L的金属管放在地面,管口正上方高h处有一小球自由下落,已知重力加速度为g,不计空气阻力。求小球穿过管所用时间。
 解析:
小球到达管上端的时间为
到达管下端的时间为
小球穿过管所用时间
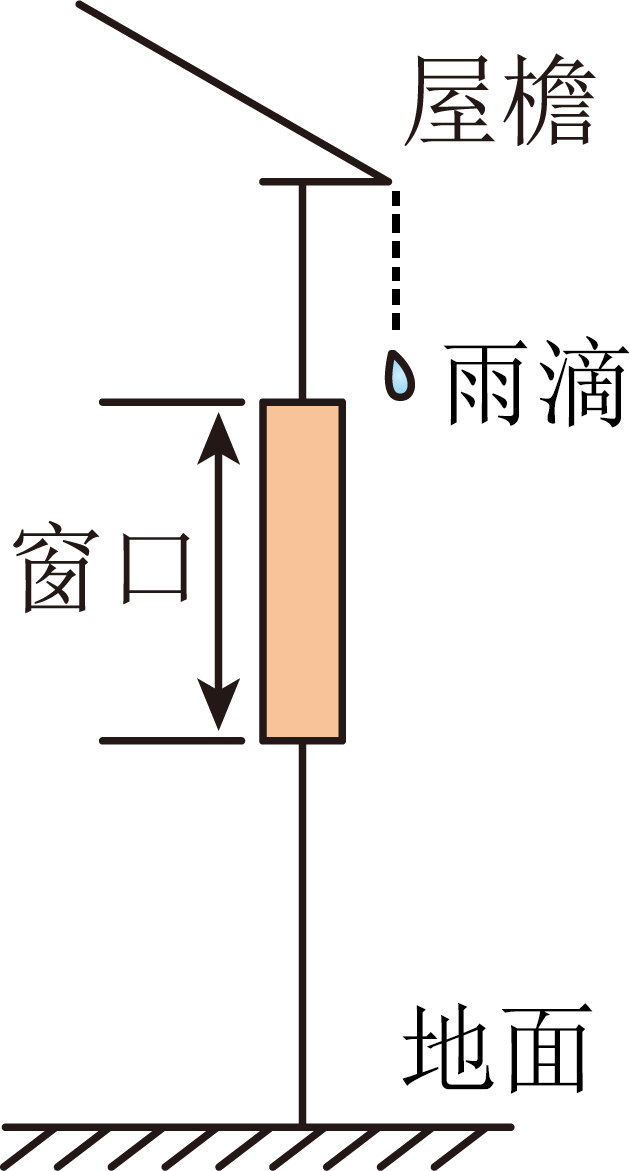
例2:下雨时,屋檐上每隔一段时间会掉下一滴雨水,其运动可看作自由落体运动,重力加速度取10m/s2。屋檐下边有一窗户,它的上下边缘高度差为1.2m,雨滴完全通过窗户(从上边檐到下边檐)的时间为0.2s。试求:
(1)雨滴落到窗子上边缘时的速度大小;
(2)屋檐距离窗户上边檐的距离;
(3)雨滴从屋檐下落到窗户中点的时间。
解析:
小球到达管上端的时间为
到达管下端的时间为
小球穿过管所用时间
例2:下雨时,屋檐上每隔一段时间会掉下一滴雨水,其运动可看作自由落体运动,重力加速度取10m/s2。屋檐下边有一窗户,它的上下边缘高度差为1.2m,雨滴完全通过窗户(从上边檐到下边檐)的时间为0.2s。试求:
(1)雨滴落到窗子上边缘时的速度大小;
(2)屋檐距离窗户上边檐的距离;
(3)雨滴从屋檐下落到窗户中点的时间。
 解析:
(1)雨滴在穿过窗户的这段运动的中间时刻速度
雨滴落到上边缘时的速度
(2)屋檐距离窗户的上边缘距离
(3)雨滴到达下边缘时的速度
雨滴在窗户中点的速度
下落到中点的时间
解析:
(1)雨滴在穿过窗户的这段运动的中间时刻速度
雨滴落到上边缘时的速度
(2)屋檐距离窗户的上边缘距离
(3)雨滴到达下边缘时的速度
雨滴在窗户中点的速度
下落到中点的时间
 解析:
小球到达管上端的时间为
到达管下端的时间为
小球穿过管所用时间
例2:下雨时,屋檐上每隔一段时间会掉下一滴雨水,其运动可看作自由落体运动,重力加速度取10m/s2。屋檐下边有一窗户,它的上下边缘高度差为1.2m,雨滴完全通过窗户(从上边檐到下边檐)的时间为0.2s。试求:
(1)雨滴落到窗子上边缘时的速度大小;
(2)屋檐距离窗户上边檐的距离;
(3)雨滴从屋檐下落到窗户中点的时间。
解析:
小球到达管上端的时间为
到达管下端的时间为
小球穿过管所用时间
例2:下雨时,屋檐上每隔一段时间会掉下一滴雨水,其运动可看作自由落体运动,重力加速度取10m/s2。屋檐下边有一窗户,它的上下边缘高度差为1.2m,雨滴完全通过窗户(从上边檐到下边檐)的时间为0.2s。试求:
(1)雨滴落到窗子上边缘时的速度大小;
(2)屋檐距离窗户上边檐的距离;
(3)雨滴从屋檐下落到窗户中点的时间。
 解析:
(1)雨滴在穿过窗户的这段运动的中间时刻速度
雨滴落到上边缘时的速度
(2)屋檐距离窗户的上边缘距离
(3)雨滴到达下边缘时的速度
雨滴在窗户中点的速度
下落到中点的时间
解析:
(1)雨滴在穿过窗户的这段运动的中间时刻速度
雨滴落到上边缘时的速度
(2)屋檐距离窗户的上边缘距离
(3)雨滴到达下边缘时的速度
雨滴在窗户中点的速度
下落到中点的时间4、非质点的自由落体
例1:如图所示,用绳拴住木棒AB的A端,使木棒在竖直方向上静止不动,在悬点A端正下方有一点C距A端0.8m.若把绳轻轻剪断,测得A、B两端通过C点的时间差是0.2s,重力加速度g=10m/s2,不计空气阻力.
(1)求木棒AB的长度
(2)D为AB棒上的一点,若AD、DB两段通过C点的时间相同,求AD长
 解析:
(1)设木棒的长度为,绳子剪断后木棒自由下落,可将A、B两端分别看做自由下落的质点,它们下落到C点所用时间分别为、。
依题意有,
联立三式解得:
(2)由于AD、DB两段通过C点的时间相同,为等时间间隔。
根据,可得:.
而且:
联立解得:
解析:
(1)设木棒的长度为,绳子剪断后木棒自由下落,可将A、B两端分别看做自由下落的质点,它们下落到C点所用时间分别为、。
依题意有,
联立三式解得:
(2)由于AD、DB两段通过C点的时间相同,为等时间间隔。
根据,可得:.
而且:
联立解得:
例2:如图所示,直棒AB长11.25m,上端为A、下端为B,在B的正下方5m处有一长度为15m,内径比直棒大得多的固定空心竖直管,手持直棒由静止释放,让棒做自由落体运动,不计空气阻力,重力加速度g=10m/s2,求:
(1)直棒下端B刚好开始进入空心管时的瞬时速度vB;
(2)直棒下端B通过空心管所用的时间;
(3)直棒在空心管中运动的时间。
 解析:
(1)直棒下端B刚好开始进入空心管时下落的高度为,
(2)设直棒下端B通过空心管所用的时间为,空心管长度为,
则有
解得
(3)设直棒在空心管中运动的时间为,直棒长度为,
则有
解得
解析:
(1)直棒下端B刚好开始进入空心管时下落的高度为,
(2)设直棒下端B通过空心管所用的时间为,空心管长度为,
则有
解得
(3)设直棒在空心管中运动的时间为,直棒长度为,
则有
解得
5、两个物体自由下落
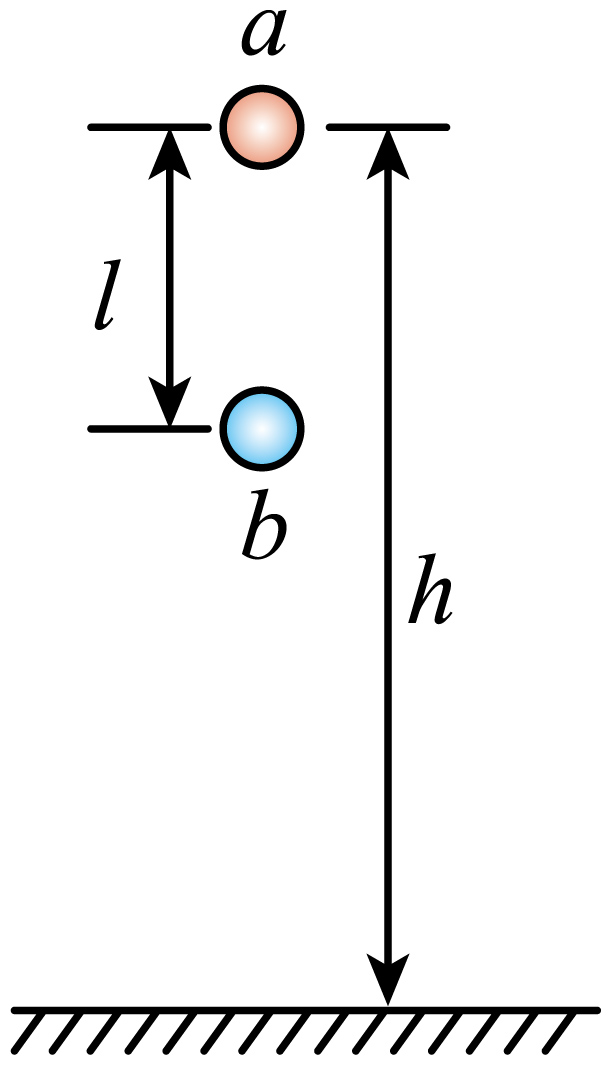
例1:如图所示,两个小球a、b的质量分别为ma、mb,且ma>mb,两球竖直方向相距l,小球a距离地面的高度为h。现让小球a、b由静止同时释放,两个小球相继落地的时间间隔为∆t,不计空气阻力,下列说法中正确的是( )
解析:
对于不同高度同时释放的小球,因为,,两物体的运动时间都是一样的,所以速度和位移都一样。
两者会保持相对距离l一直不变落地。
对a来说,落地时间
对b来说,落地时间
可知,l越大,Δt越大,h越大,Δt越小。
故选D。
如果两个物体先后释放,我们可以利用v-t图像来解决问题。
例2:下雨时雨水从屋檐滴落是生活中常见的现象,假设屋檐某一位置每隔相同的时间无初速滴落一滴雨滴,不计空气作用力,则已滴出且未落地的相邻雨滴之间的( )
A.距离保持不变 B.距离越来越大
C.速度之差越来越小 D.速度之差越来越大
解析:
 从v-t图像可以看出,两物体的速度之差一直不变,但是相对距离(两图像中间围成的面积)越来越大。
故选D。
从v-t图像可以看出,两物体的速度之差一直不变,但是相对距离(两图像中间围成的面积)越来越大。
故选D。

| A.a有可能先落地 | B.a下落的加速度比b大 |
| C.l越大,∆t越小 | D.h越大,∆t越小 |