normalen op een ovaal en een ellips
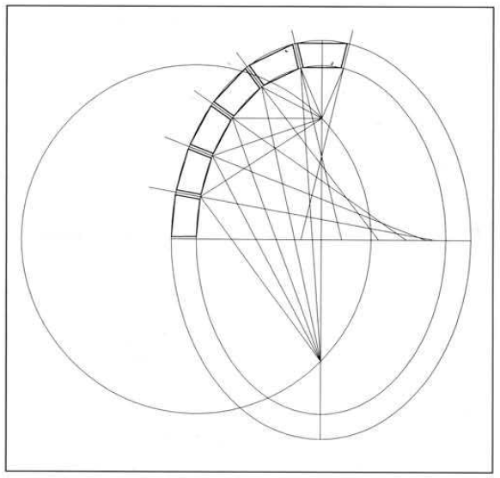
normalen op een ovaal
Riccardo Miglari gaat in zijn artikel Ellissi e ovali, epilogo di un conflitto in op het vormverschil tussen ovaal en ellips. Een ovaal is opgebouwd uit cirkelbogen. Loodrechten vanuit punten op de omtrek van een ovaal gaan dus door de middelpunten van de cirkelbogen.
normalen op een ellips
Maar een ellips is niet opgebouwd uit cirkelbogen. Meer nog, de ellips is een kromme waarvan de kromming voortdurend verandert. Het gevolg is dat normalen op een ellips niet door één punt (of eventueel de twee brandpunten) gaan.
Teken je een rij normalen op een ellips dan tekent zich een vlakke kromme af, de evolute van de ellips.
kromming
Ovalen zijn dus niet enkel eenvoudiger om te construeren, ze zijn ook veel praktischer om te gebruiken in de architectuur.
- Wil je bijvoorbeeld een plein omringen door een colonnade, dan moet je normalen construeren op de kromme. Voor een ovaal is dat geen probleem, want de stralen van een cirkel gaan door het middelpunt. Bij een ellips daarentegen moet je elke normaal apart construeren.
- Wil je een ellips realiseren in steen, dan moet je elke steen een verschillende vorm geven omdat in elk punt van een ellips de kromming anders is. In een ovaal heeft elk punt van dezelfde cirkelboog dezelfde kromming.
Het is net aan deze kromming dat je een ovaal en een ellips uit elkaar kunt houden. Een geoefend oog merkt meestal dat een ovaal 4 (of meer) punten heeft waar de kromming verandert.
Bij historische gebouwen is dat echter vaak niet eenvoudig. Een koepel bouw je niet zonder enige onnauwkeurigheid en doorheen de tijd kan een koepel zettingsverschillen vertonen. Leg dit naast het geringe verschil tussen een ovaal en een ellips en je stelt al snel vast dat meten geen uitsluitsel geeft.
Kijk je zonder kennis van bronnenonderzoek, architectuurpraktijk en -geschiedenis naar een gebouw, dan verval je inderdaad opnieuw in de ambiguïteit en discussies over ovalen en ellipsen.