0-v-0模型
所谓模型，指的是一类很典型的运动问题：物体由静止以加速度做匀加速直线运动，经过时间加速到后，立即以加速度减速，又经过时间后减速到0。
从图像我们可以得到：
若已知总位移为，我们由和上述比例式可得：
若已知总运动时间为，我们由和上述比例式可得：
例1：(多选)汽车由甲地开出，沿平直公路开到乙地时，刚好停止运动.它的速度－时间图像如图所示.在和两段时间内，汽车的( )
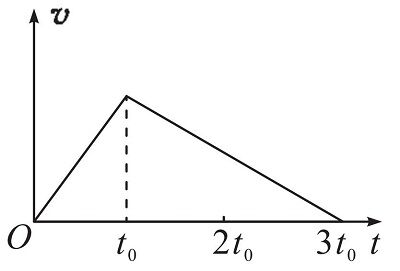A.加速度大小之比为2∶1
B.位移大小之比为1∶2
C.平均速度大小之比为2∶1
D.平均速度大小之比为1∶1
解析：
假设最大速度为，
选B、D
A.加速度大小之比为2∶1
B.位移大小之比为1∶2
C.平均速度大小之比为2∶1
D.平均速度大小之比为1∶1
解析：
假设最大速度为，
选B、D例2：质点由A 点出发沿直线AB 运动，行程的第一部分是加速度大小为的匀加速运动，接着做加速度大小为的匀减速运动，到达B 点时恰好速度减为零.若AB 间总长度为，则质点从A 到B 所用时间t为( )
A. B. C. D.
解析：
设物体加速阶段的时间为，运动位移；减速阶段的运动时间，运动位移。
联立解得
又，
故选B
例3：一汽车由静止沿直线由A 行驶至B，汽车先做匀加速直线运动再做匀减速直线运动，到达B 时速度恰好减至零，已知A、B 间相距300m，行驶时间为60s，分析汽车行驶的最大速度.
解析：
假设最大速度为，
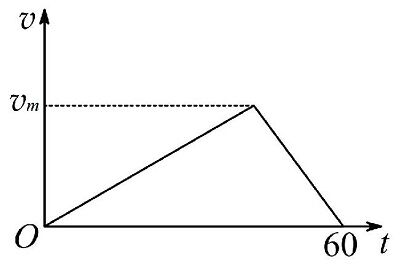由图像我们可以知道，，
由图像我们可以知道，，例4：一辆汽从A到B，先匀加速后匀速再匀减速，要求汽车从A静止开始运动，到B刚好速度为，已知汽车加速和减速时加速度都为,AB间距离为,求汽车行驶的最短时间（不考虑汽车的最大速度）。
解析：
要使汽车的行驶时间最短，加速时间要尽可能长，匀速阶段应该尽量少，所以整个过程应该只包含加速和减速阶段。
假设加速阶段时间为，减速阶段时间
解得
则汽车行驶最短时间为