Introducción
¿Por qué se debe estudiar la probabilidad condicionada?
Una vez hemos entendido algunas ideas clave como sucesos, espacio muestral y Regla de Laplace, es hora de estudiar el concepto de probabilidad condicionada. El estudio de la probabilidad condicionada es fundamental en esta rama de las Matemáticas, puesto que nos permite entender cómo ocurren sucesos dentro de un contexto específico, dado que ya ha sucedido otro suceso. Esto es crucial en situaciones donde la información disponible afecta la probabilidad de un resultado.
Notación
Denotaremos por P(A|B) a la probabilidad de que ocurra el suceso A sabiendo que ha ocurrido B. Estudiaremos cómo calcular la probabilidad condicionada en el siguiente apartado.
Ejemplo
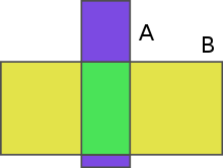
En la imagen anterior tenemos dos sucesos A (representado por un rectángulo azul) y B (representado por un rectángulo amarillo). Además, su intersección se representa mediante un rectángulo verde. La probabilidad condicionada P(A∣B) mide qué tan probable es A dentro del suceso B.