弹力（二）
四、弹簧、橡皮筋的弹力与胡克定律
对于弹簧、橡皮筋之类的有明显形变的物体，他们产生的弹力可以根据其形变的方向和大小来判断。
弹簧可以拉伸也可以压缩，所以它产生的弹力有两个方向，拉伸的时候，弹力沿弹簧向内；压缩的时候，弹力沿弹簧向外。总之，这个力的方向与形变方向相反。
在弹性限度以内，弹簧弹力的大小与弹簧的形变量成正比，即，这个规律是一个叫胡克的科学家发现的，所以也叫胡克定律。
我们一般用或者来表示弹簧的原长，即不受外力时弹簧的自然长度，用或者来表示弹簧被拉伸或压缩后的长度。形变量或。
如果是橡皮筋，它只在被拉伸时能用胡克定律计算弹力，被压缩时和绳子一样没有弹力。
弹力和形变量之间的比例系数叫做弹簧的劲度系数，劲度系数表示弹簧的软硬程度，劲度系数越小，弹簧越软，越容易被拉开；劲度系数越大，弹簧越硬，越不容易被拉开。
弹簧的劲度系数只与弹簧的材料、粗细、缠绕方式等有关，与拉力和形变量没有关系。
弹簧的劲度系数可以在实验中测得。
我们测出弹簧的长度和对应的拉力或者压力，作出图像，图像的斜率就表示弹簧的劲度系数。
注意区分以下两种图像，有的图像记录的是弹簧的长度，而有的图像记录的是形变量。
例1：已知某弹簧原长为16cm，可拉伸或压缩，其弹力
与伸长量
的关系图线如图所示，关于该弹簧的说法正确的是（ ）
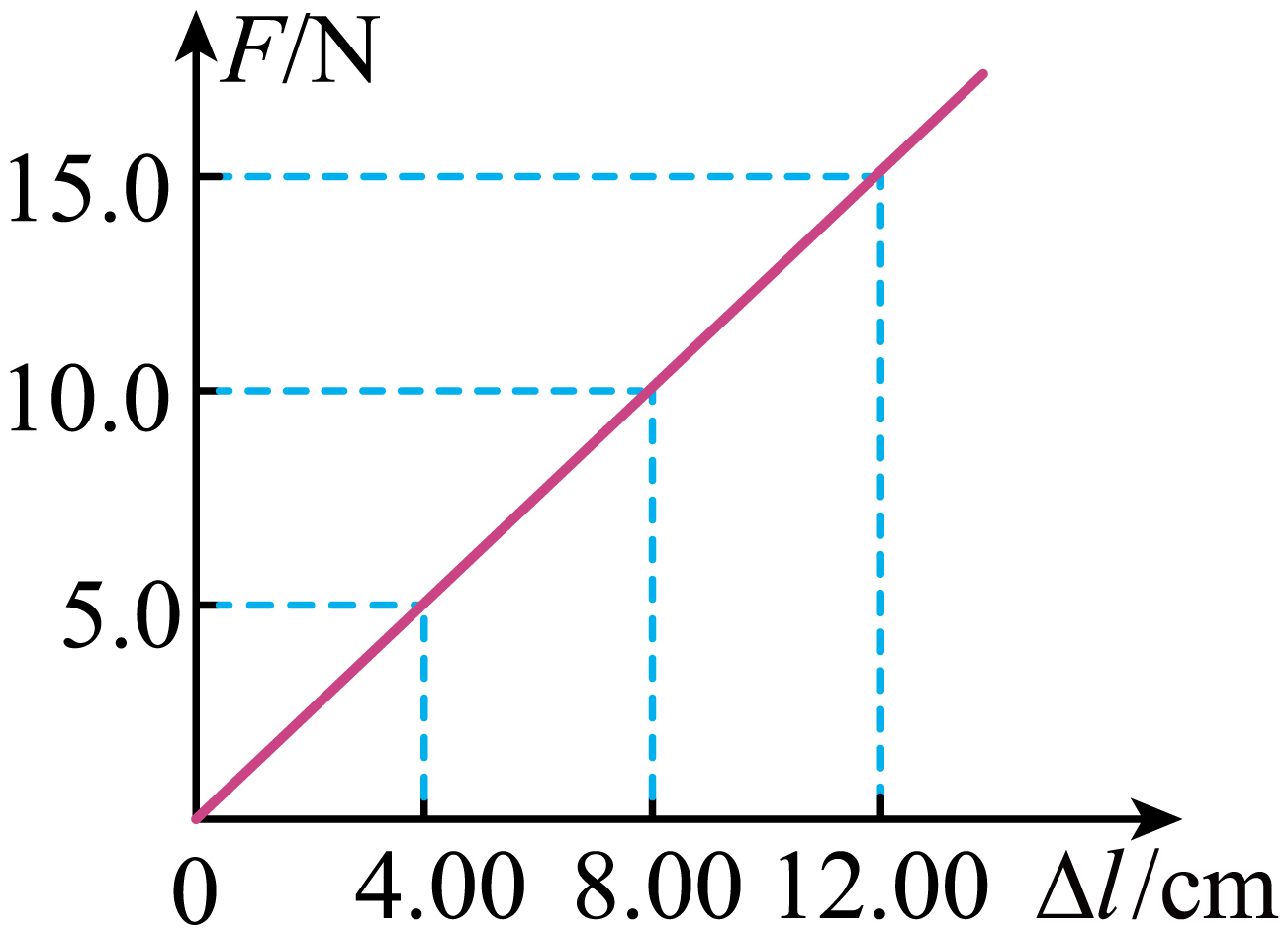
解析：
弹簧的弹力是与形变量成正比而不是长度，A错
弹簧劲度系数，B错
弹簧长度为时，形变量为，读图知，弹力大小为，C对
劲度系数与弹簧的材质、粗细等有关，与所受拉力无关，D错
与伸长量的关系图线如图所示，关于该弹簧的说法正确的是（ ）
| A．弹力与弹簧的长度成正比 |
B．该弹簧劲度系数为 |
| C．当弹簧长度为12cm时，弹力为5.0N |
| D．当弹簧受到的拉力为0时，劲度系数为0 |
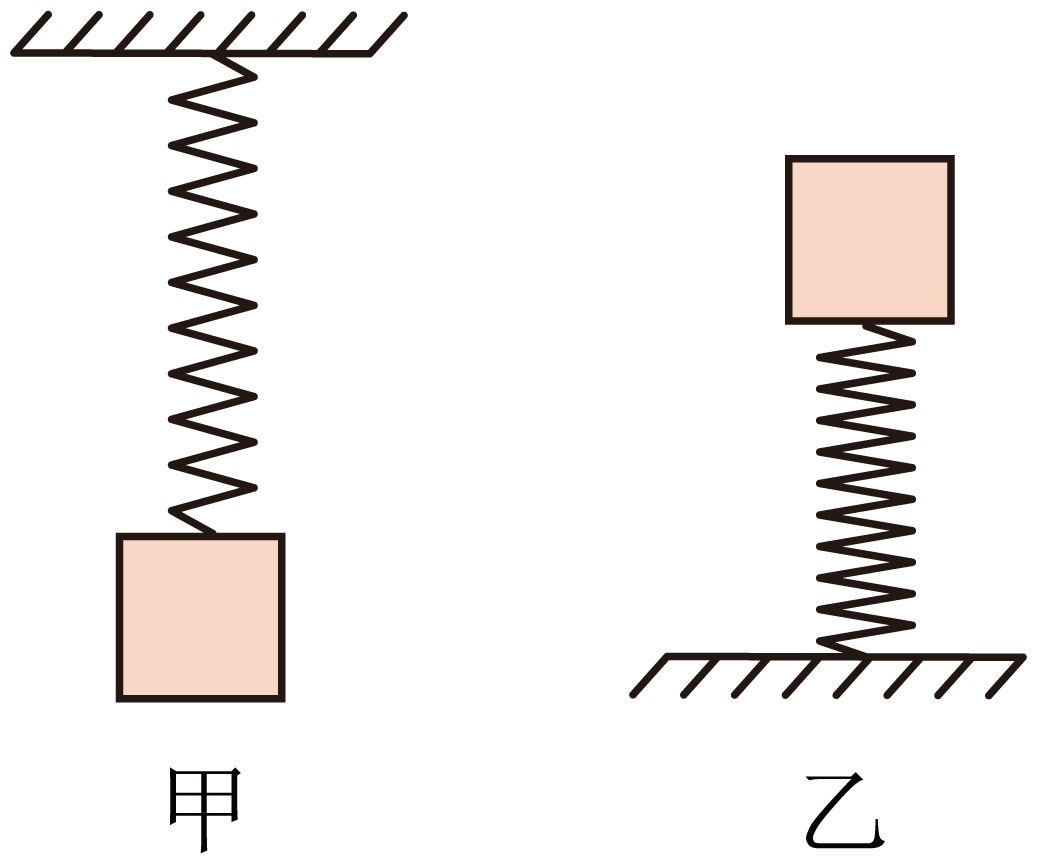
例2：如图甲所示，质量
的物块用轻质弹簧悬挂在水平天花板上，物块静止时弹簧的长度
。如图乙所示，将该物块置于固定在水平地面上的同一弹簧上端，物块静止时弹簧的长度
。取重力加速度大小
。弹簧始终处于弹性限度内。求：
(1)弹簧的劲度系数k和原长
；
(2)弹簧的弹力大小
时弹簧的长度
。
解析：
（1）物块重力
甲图中，弹簧弹力
乙图中，弹簧弹力
联立解得：
此题，我们还可以用来计算
（2）弹簧形变量
因为不知道弹簧是被压缩还是拉伸，所以
或
的物块用轻质弹簧悬挂在水平天花板上，物块静止时弹簧的长度。如图乙所示，将该物块置于固定在水平地面上的同一弹簧上端，物块静止时弹簧的长度。取重力加速度大小。弹簧始终处于弹性限度内。求：
(1)弹簧的劲度系数k和原长；
(2)弹簧的弹力大小时弹簧的长度。
解析：
（1）物块重力
甲图中，弹簧弹力
乙图中，弹簧弹力
联立解得：
此题，我们还可以用来计算
（2）弹簧形变量
因为不知道弹簧是被压缩还是拉伸，所以
或
五、弹簧的串并联
弹簧和绳子是一样的，一端的弹力会沿着弹簧传到另一端，对轻弹簧来说，弹簧上的弹力处处相等。
当两条弹簧串联在一起后，受到的弹力相等。
两条弹簧受到弹力产生的形变量，为两条弹簧分别在这个弹力作用下的形变和之和。
当两条弹簧并联在一起后，他们的形变将一样，这时两根弹簧上的弹力大小因劲度系数而异。
设两根弹簧上的弹力分别为和，此时有，总弹力。
例1：如图所示，两劲度系数均为20N/cm的轻质弹簧a、b串接在一起，a弹簧的一端固定在墙上，开始时两弹簧均处于原长状态，现用水平向右F=20N的力作用在b弹簧的P端，达到平衡时P端向右移动的距离为（ ）
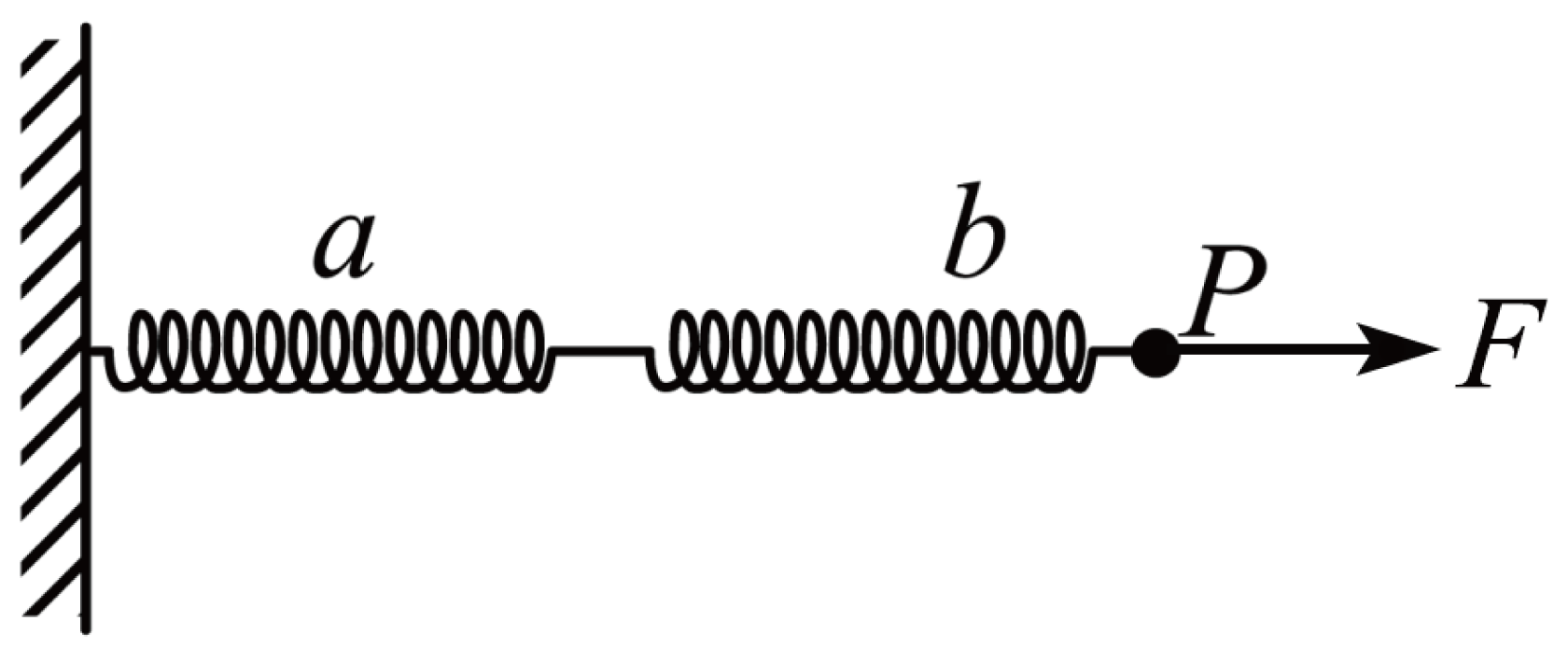
解析：
弹簧串联时，受力相同，均会移动，一共移动2cm，选B
例2：（多选）某人用来锻炼身体的拉力器并列装有三根相同的弹簧，每根弹簧的自然长度都是40 cm，一次锻炼时，他用600 N的力把弹簧拉长至1.4 m，如图所示，则（ ）
解析：
三根弹簧并联且劲度系数相同，弹簧弹力会均分600N拉力，每根弹簧上的拉力都是200N，A错B对。
单根弹簧的劲度系数，C对D错。
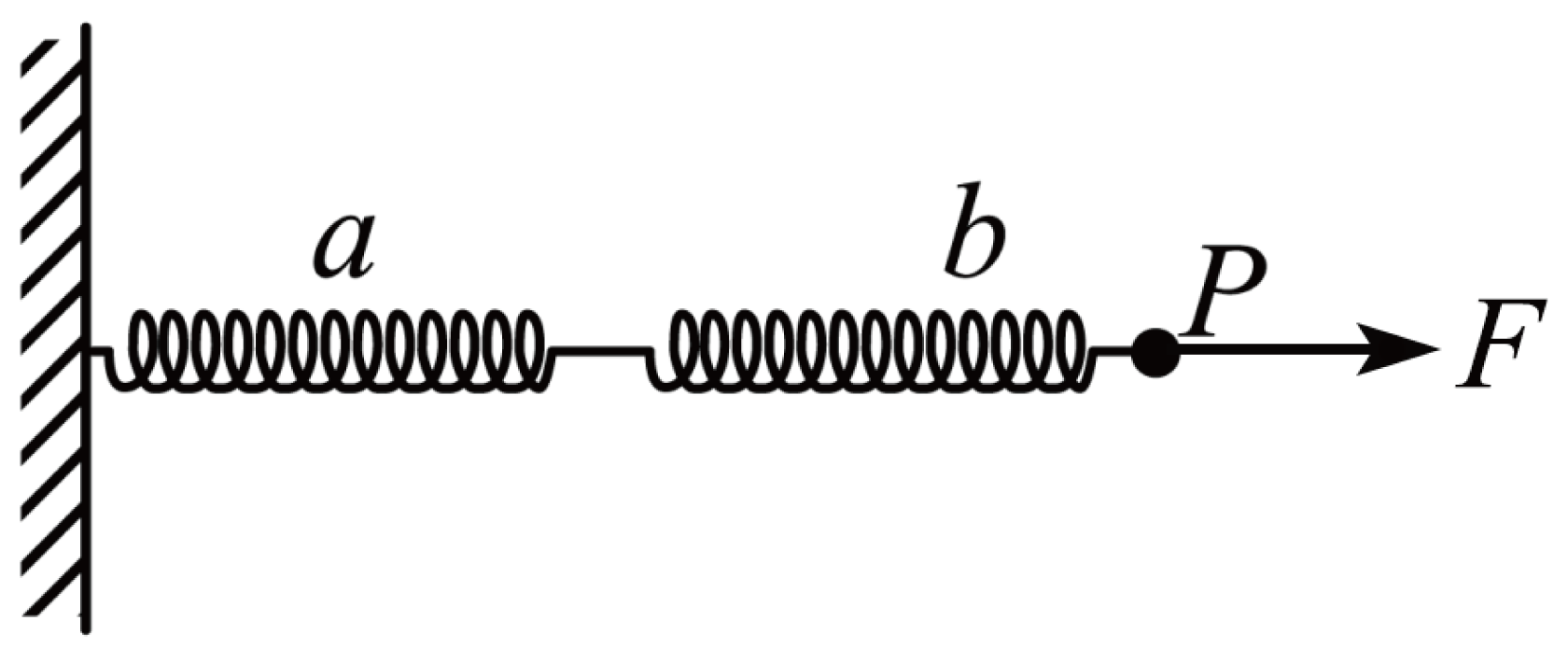
| A．1cm | B．2cm | C．3cm | D．4cm |
| A．每根弹簧产生的弹力为600 N | B．每根弹簧产生的弹力为200 N |
| C．每根弹簧的劲度系数为200 N/m | D．每根弹簧的劲度系数为600 N/m |
弹簧的串联要求两根弹簧直接相连或者用轻绳之类质量不计的物体相连，如果两根弹簧中间还有重物，不属于弹簧的串联，也不能用两根弹簧上弹力相等的结论。
此时需要单独对每根弹簧进行分析。
例3：如图所示，a、b两物体通过轻弹簧P栓接，轻弹簧Q上端与物体b栓接，下端与水平地面接触但不栓接，两物体及两轻弹簧在同一竖直线上且均处于静止状态。a、b两物体重量均为G、P、Q两轻弹簧劲度系数均为k，且两轻弹簧始终在弹性限度内。现对物体a施加一竖直向上的力，使其缓慢上升，轻弹簧Q下端脱离地面瞬时，物体a上升的高度为（ ）
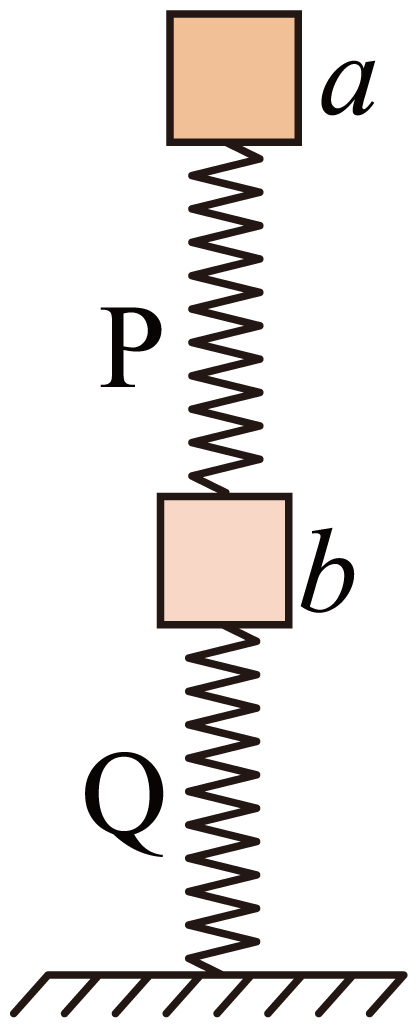
解析：
没有施加拉力时，
Q弹簧受到2G的压力压缩，形变量
P弹簧受到G的压力压缩，形变量
施加拉力至Q脱离地面时，
Q弹簧无弹力，恢复原长
P弹簧受弹力G拉伸，形变量
P弹簧向上移动
Q弹簧向上移动
物体a一共上升，选D
A． | B． |
C． | D． |