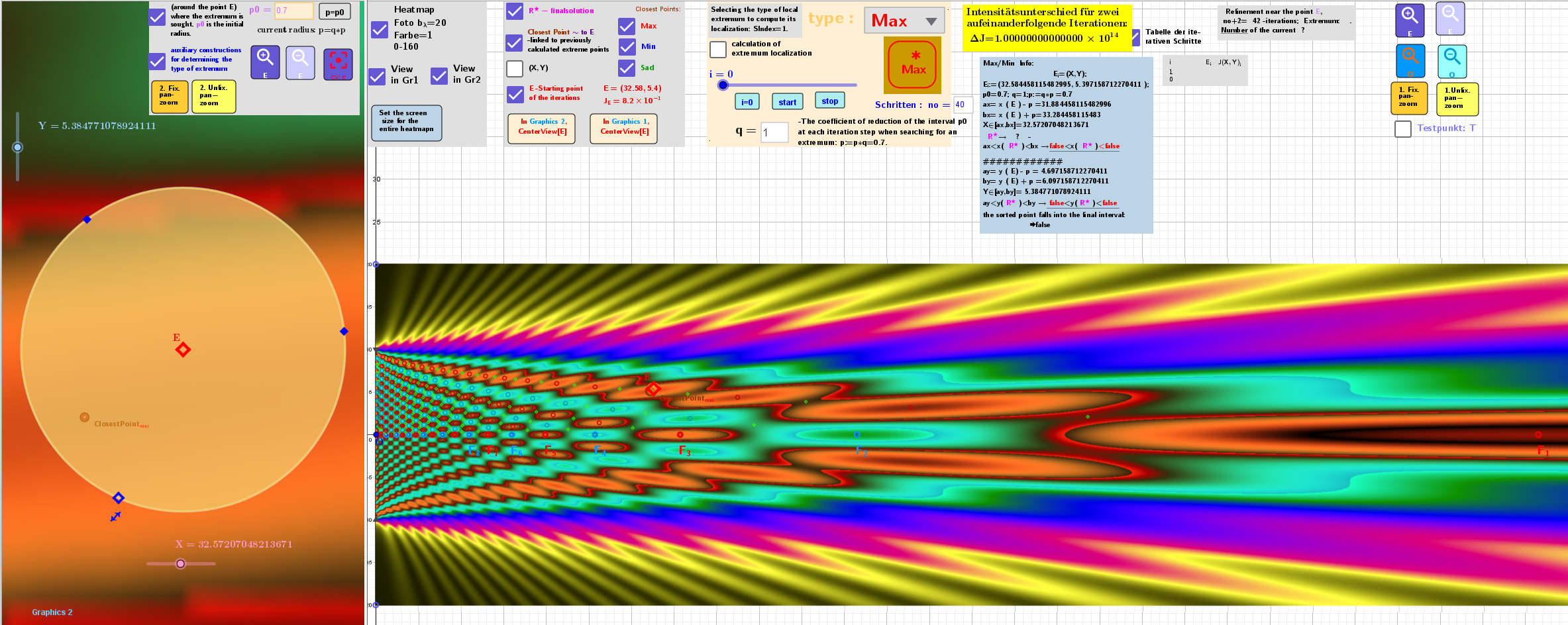
Applet of the proposed coordinate descent-ascent algorithm for computing stationary points of a numerically specified function
A stationary point of a function of two (or multiple) variables is a point at which all partial derivatives are zero and can be a local maximum, minimum, or saddle point.
As a numerically specified function, we consider the intensity distribution of the diffraction field when light is diffracted by a single slit: J=J(x,y). The order of operations is the same as for the explicit set function discussed in applet 1. The algorithms for finding max / min can be found in applet 2, and the algorithm for finding a saddle point can be found in applet 3. Algorithm for finding the expected locations of Local maxima, minima or saddle points of stationary points of a numerical function of two variables in the coordinate descent-ascent method in 4.

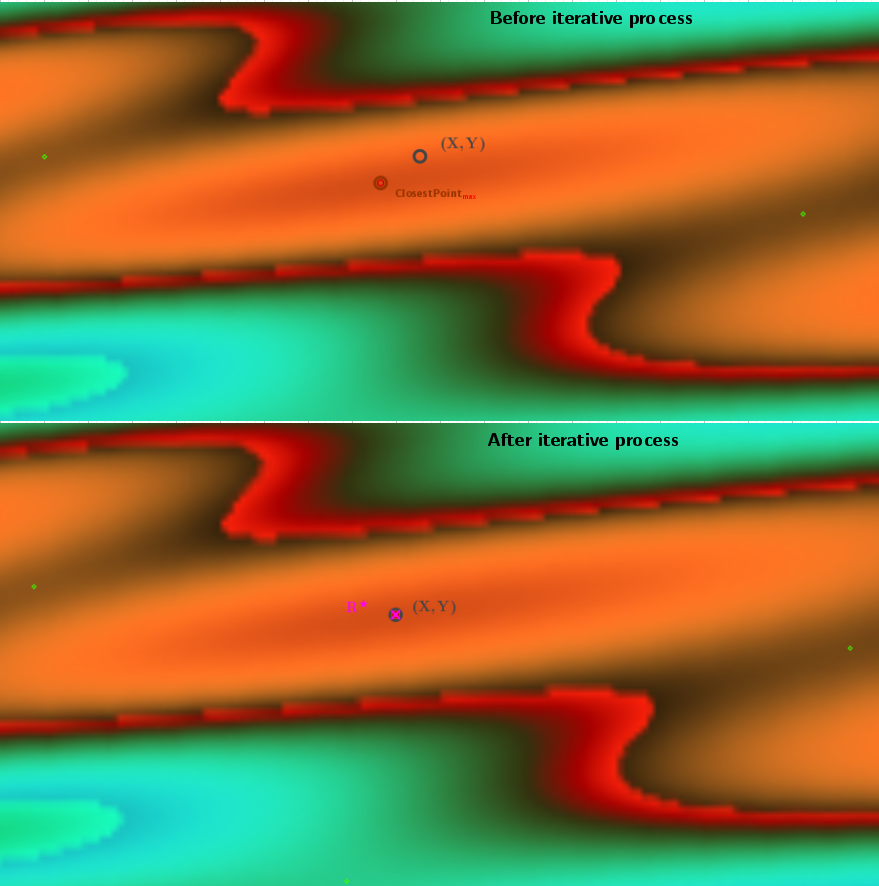
* Some Images of the applet of the application of the descent-ascent algorithm of coordinates for the calculation of stationary points of the numerical function f(x,y) in the case of finding a saddle point can be found in the applet.