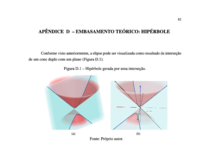
Hipérbole
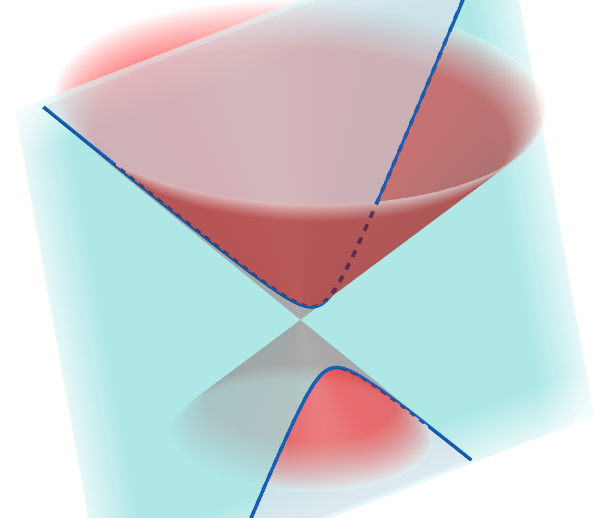
Construindo a hipérbole do mesmo modo que Apolônio, através da intersecção de um plano com um cone duplo, teremos o seguinte lugar geométrico.
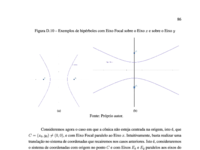
Agora vamos continuar investigando a equação da elipse.
O que acontece quando eu mudo o sinal da soma para a subtração?
Utilize a janela de interação a seguir, inserindo a equação da elipse, modificando o sinal de "+" pelo sinal de "-".
Lembrando que a equação da elipse é:
Que curva surgiu? Veja a definição a seguir.
Seja o lugar geométrico dos pontos no plano cartesiano tal que o módulo da diferença entre e dois pontos fixos é constante, ou seja, .
Vamos nomear esses dois pontos fixos de e , eles podem ser dois pontos quaisquer distintos do plano. Estes pontos são chamados de focos.
Agora é a sua vez de construir o gráfico, dessa vez vamos utilizar um recurso que permite construir uma hipérbole com três pontos.
1) No canto superior são ícone de "Ferramentas", no sétimo são as "Cônicas" 
, clique em "Hipérbole"
.
2) Selecione "", "" e "", nesta ordem.
3) No canto superior esquerdo clique na seta 
.
4) Mova o ponto "" para verificar o que acontece com a hipérbole.
, clique em "Hipérbole".
2) Selecione "", "" e "", nesta ordem.
3) No canto superior esquerdo clique na seta .
4) Mova o ponto "" para verificar o que acontece com a hipérbole.Nesta construção você tem uma liberdade maior para manipular os pontos e verificar o que acontece quando altera-se os focos da hipérbole. Até o momento não trabalhamos com equações então verifique na janela a seguir o que a definição nos mostra. Ou seja, visualize dinamicamente que é o módulo da diferença entre e dois pontos fixos é constante.
1) Fixados os focos "" e "", mova o ponto "" e observe o valor da distância.
2) Mova "" e "" verifique se o valor da distância se alterou e repita o passo 1.
Note que, com os focos fixos, o módulo da diferença entre as distância permanece constante mesmo que o ponto P seja alterado ao longo desta hipérbole. Porém, se alterarmos a posição dos focos, daí teremos outra hipérbole e, por isso, o módulo das distâncias poderá apresentar outro valor.
Equação da hipérbole
A partir da definição de hipérbole chegamos a equação reduzida de modo muito análogo realizado com a elipse.
Novamente temos dois caminhos que fica a cargo do leitor escolher. Diretamente a "fórmula" chamada de equação reduzida da hipérbole ou deduzi-la através da definição. Caso queria conhecer a demonstração matemática, clique no arquivo a seguir, caso contrário continuemos.
Demonstração da hipérbole
Os valores de e são reais, com e diferentes de zero, portanto é comum aparecer radicais, pois os valores são elevados ao quadrado eliminando a raiz.
Note que a equação da elipse e da hipérbole são muitos parecidas, diferenciando apenas no sinal entre os dois termos que envolvem as variáveis e .
Continuando a investigação da equação reduzida da hipérbole, surge duas perguntas. O que acontecerá se trocarmos a posição do com ? Se variar o e ?
Na janela a seguir, construa duas hipérbole para que possa compará-las, seguindo os seguintes passos:
1) Escreva a equação reduzida da hipérbole com os termos e . Perceba que automaticamente o GeoGebra adicionará os controles deslizantes.
2) Escreva uma nova equação trocando o lugar do com . Além disso, no lugar de escreva e no lugar de escreva , perceba que automaticamente o GeoGebra adicionará os controles deslizantes.
3) Deslize os controles para verificar o que está acontecendo com a cônica.
Note que as duas hipérboles estão com cores diferentes, caso queira uma melhor visualização, no canto esquerdo tem a possibilidade de ocultar uma das hipérboles, apertando na bolinha.
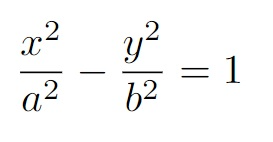
Recomendação
Tome nota em seu caderno para que não perca algumas informações importantes.
1) Desenhe em seu caderno como é o gráfico quando o coeficiente de é negativo.
2) Desenhe em seu caderno como é o gráfico quando o coeficiente de é negativo.
Se ainda tem dúvidas volte na última janela de interação e compare.
Translação do eixo focal
Nos exemplos que trabalhamos com a hipérbole o eixo focal onde os focos e estão localizados, coincide com os eixos do plano cartesiano. Veremos que é possível que esse eixo focal não esteja sobre os eixos cartesianos. Para que isso aconteça faremos um processo semelhante ao da elipse, que foi abordado na seção anterior.
Caso queira entender como encontrar esta equação clique no arquivo a seguir.
Demonstração hipérbole transladada
Realizando um pensamento análogo que fizemos na elipse, vamos graficar a equação a seguir, lembrando que e são números diferentes de zero.
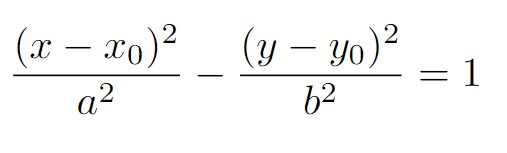
Esta equação permite que você desloque a hipérbole para qualquer lugar do seu plano cartesiano, então construa na janela a seguir, seguindo os seguintes passos.
1) Ao lado esquerdo digite a equação reduzida que acabamos de encontrar com e .
2) Utilize os controles deslizantes para verificar o que acontece com a hipérbole.
Agora responda as perguntas a seguir?
O que acontece quando altera-se os valores de ?
O que acontece quando altera-se os valores de ?