Função Afim
DEFINIÇÃO
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= a.x + b para todo x ∈ R, onde a ≠ 0.
SIGNIFICADO DOS COEFICIENTES
Na função f(x)= a.x + b, o número a é chamado de coeficiente de x, enquanto o número b é chamado de termo constante.
Veremos mais a frente que os coeficientes a e b nos ajudam a identificar o gráfico da função.
Exemplos de funções afim e seus coeficientes:
a) f(x) = 2x + 3, onde a=2 e b=3
b) f(x) = -3x + 10, onde a=-3 e b=10
c) f(x) = x + 13, onde a=1 e b=13
GRÁFICO DE UMA FUNÇÃO AFIM
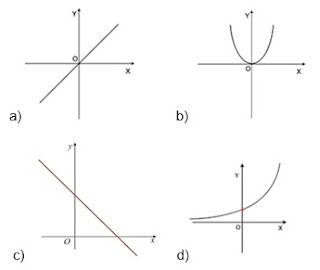
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação y = ax + b, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
Observe:
.jpg)
Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
Função decrescente: à medida que os valores de x aumentam, os valores correspondentes de y diminuem.
Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
Função decrescente: à medida que os valores de x aumentam, os valores correspondentes de y diminuem. Rápido e Fácil | Função do 1º grau | Função afim
Exercícios
1)A raiz da função afim f(x) = - 8x + 24 é:
a) 3.
b) 16.
c) – 3.
d) – 16.
2) Qual dos gráficos a seguir representa uma função do 1° grau crescente?
3) O professor de Sávio desenhou o seguinte gráfico na lousa:
A respeito do gráfico, pode-se afirmar que:
a) o gráfico representa uma função afim decrescente.
b) a raiz da função é 2.
c) o valor do coeficiente b é -3, pois a reta intercepta o eixo x no ponto (-3,0).
d) a raiz da função é – 3 e o coeficiente b vale 2
A respeito do gráfico, pode-se afirmar que:
a) o gráfico representa uma função afim decrescente.
b) a raiz da função é 2.
c) o valor do coeficiente b é -3, pois a reta intercepta o eixo x no ponto (-3,0).
d) a raiz da função é – 3 e o coeficiente b vale 2