Grenzwerte im Unendlichen
Betrachte die Graphen der drei Funktionen f, g und h. (Beachte die verschiedenen Skalen der x-Achsen bei den Graphen oben und unten.)
Vergleiche das Verhalten der drei Funktionen für immer größer werdende x-Werte („x gegen
unendlich“; „“ ).
Formuliere jeweils eine Charakterisierung dieses Verhaltens.

Für immer größer werdende x-Werte...
Man schreibt: 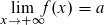 (hier: 2)
Man sagt: "Der Limes (Grenzwert) von f(x) für x gegen unendlich ist a. Die Funktion konvergiert gegen a."
(hier: 2)
Man sagt: "Der Limes (Grenzwert) von f(x) für x gegen unendlich ist a. Die Funktion konvergiert gegen a."
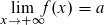 (hier: 2)
Man sagt: "Der Limes (Grenzwert) von f(x) für x gegen unendlich ist a. Die Funktion konvergiert gegen a."
(hier: 2)
Man sagt: "Der Limes (Grenzwert) von f(x) für x gegen unendlich ist a. Die Funktion konvergiert gegen a."Für immer größer werdende x-Werte...
Man schreibt: 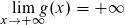 Man sagt: "Der Limes (Grenzwert) von g(x) für x gegen unendlich ist . Die Funktion divergiert bestimmt."
Man sagt: "Der Limes (Grenzwert) von g(x) für x gegen unendlich ist . Die Funktion divergiert bestimmt."
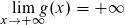 Man sagt: "Der Limes (Grenzwert) von g(x) für x gegen unendlich ist . Die Funktion divergiert bestimmt."
Man sagt: "Der Limes (Grenzwert) von g(x) für x gegen unendlich ist . Die Funktion divergiert bestimmt."Für immer größer werdende x-Werte...
Man sagt: "Der Limes (Grenzwert) von h(x) für x gegen unendlich existiert nicht. Die Funktion divergiert unbestimmt."
Ordne den Graphen die unten aufgeführten Funktionsterme zu.
Zur Auswahl stehende Funktionsterme:

Der zugehörige Graph zum Funktionsterm (I) ist
Der zugehörige Graph zum Funktionsterm (II) ist
Der zugehörige Graph zum Funktionsterm (III) ist
Der zugehörige Graph zum Funktionsterm (IV) ist
Der zugehörige Graph zum Funktionsterm (V) ist
Bestimme anschließend die Art des Verhaltens für und für und den Grenzwert.