Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

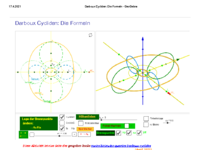
Darboux Cycliden: Die Formeln

Author:Walter Füchte

Diese Aktivität ist eine Seite des geogebra-books conics bicircular-quartics Darboux-cyclides (April 2021) Diese Aktivität ist auch eine Seite des geogebra-books Moebiusebene

Eine Darboux Cyclide ist eine implizit definierte Fläche mit einer Gleichung des Typs:
  • mit linearem und quadratischem , jeweils mit reellen Koeffizienten
Die reell 12-dimensionale Klasse dieser Fläche ist invariant unter räumlichen Möbiustransformationen. Jede solche Fläche besitzt mindestens eine Symmetrie-Kugel, dh. eine Kugel, an welcher gespiegelt die Fläche invariant ist. 1)s.u. Wählt man eine solche Symmetrie-Kugel als (komplexe) Koordinaten-Ebene, so ist die Schnittkurve eine bizirkulare Quartik. Bizirkulare Quartiken lassen sich charakterisieren über die Anzahl der paarweise orthogonalen Symmetrie-Kreise. 2) Im obigen Applet ist die bizirkulare Schnittkurve 2-teilig, mit einer geeigneten Möbiustransformation erreicht man, dass die Cyclide symmetrisch zu den Koordinatenebenen, zur Einheitskugel und zu einer weiteren orthogonalen imaginären Kugel liegt 4). Die Gleichung der Cyclide reduziert sich auf
Wir betrachten die Koordinatenebenen als komplexe Gausssche Zahlenebenen, damit vereinfachen sich viele Rechnungen. Punkte, welche für die Cyclide eine Rolle spielen, treten wegen der Symmetrieen in den Ebenen stets als Quadrupel auf: , von den wenigen Ausnahmen abgesehen. Leider kennen wir für diese Darboux Cycliden keine Parameterdarstellung 5). Schnittpunkte mit den Koordinatenachsen:
  • ,, mit ergeben sich die Schnittpunkte mit der -Achse .
Schnittpunkte mit den Einheitskreisen in den Koordinatenebenen:
  • liefert die Schnittpunkte mit dem Einheitskreis der -Ebene; entsprechend berechnet man die Schnittpunkte mit den Einheitskreisen der anderen Koordinatenebenen, sofern sie existieren.
Brennpunkte: Einzelne Darboux Cycliden gehören stets zu einer Schar konfokaler Darboux Cycliden: gemeinsam sind die 3*4 Brennpunkte, zusammenfallende Brennpunkte mitgezählt.
  • Mit berechnet man das Brennpunkt-Quadrupel in der -Ebene. Diese Rechnung liefert komplex die Brennpunkte auch dann, wenn sie auf dem Einheitskreis liegen!!
  • Sind die Brennpunkte bekannt, so kann man berechnen: .
Zu den fantastischen Möglichkeiten, in geogebra komplex zu rechnen, siehe die Hinweise und Bemerkungen unten! 3) Für die - und die -Ebene wurden oben die zugehörigen bizirkularen Schnittquartiken in der -Ebene dargestellt. Deren Brennpunkte berechnen sich mit Hilfe der entsprechenden Formeln für und . Die Brennpunkte müssen in die zugehörigen Koordinatenebenen gedreht werden. Leider unterstützt geogebra keine impliziten Kurven in der - bzw. der -Ebene. Implizite Kurven in der -Ebene lassen sich in den Raum verschieben, aber nicht drehen. Die Höhenlinien sind verschobene implizite Kurven, die bizirkularen Quartiken in den anderen Ebenen sind als Ortskurven erzeugt - und daher manchmal etwas instabil! Man variiere im Applet oben die Koeffizienten (fs-Fix entsperren!) und beobachte die Brennpunkte. Die Koeffizienten bestimmen die Lage der Brennpunkte. Diese sind entscheidend für die Form und die Eigenschaften der Darboux Cyclide! Geometrische Bedeutung der Brennpunkte: Eine bizirkulare Quartik besitzt 4 Brennpunkte. Wenn sie verschieden sind, kann man sie auf 3 Arten in 2 Brennpunkt-Paare zerlegen. Jede solche Zerlegung bestimmt 2 elliptische Kreisbüschel: ein elliptisches Kreisbüschel besteht aus den Kreisen durch die beiden Grundpunkte - hier sind das 2 der Brennpunkte. Durch jeden Punkt der Quartik geht aus jedem der 2 Kreisbüschel genau ein Kreis; die Quartik ist Winkelhalbierende dieser Kreise!
Konfokale Cycliden, Fokal-Kurven: Durch jeden Punkt des Möbiusraumes, von den Brennpunkten abgesehen, gehen genau 3 orthogonale konfokale Darboux Cycliden. Die Koordinatenebenen und die Einheitskugel zählen dabei mit. Auf den Achsen gibt es also zu fast jedem Punkt eine "echte" Darboux Cyclide durch diesen Punkt; die Brennpunkte dieser konfokalen Cyclide sind per definitionem dieselben. Wie berechnet man die zugehörigen Koeffizienten ? Mit dem Schieberegler wird oben zunächst ein -Achsenschnittpunkt (Scheitelpunkt) auf der -Achse variiert. Hiermit erhält man die Koeffizienten:
  • . Mit der oben berechneten reellen Zahl ergibt sich:
  • und, da der Scheitelpunkt auch für die -Ebene Scheitelpunkt ist:
Beachtenswert ist die auf den vielen Symmetrieen beruhenden Einfachheit und Symmetrie der Formeln. Im obigen Applet ist die Start-Lage der Cyclide so gewählt, dass durch die Scheitel auf der -Achse alle Cycliden der konfokalen Schar erreicht werden. Bei anderen Ausgangslagen kann es eintreten, dass manche Cycliden der Schar die -Achse nicht schneiden. Dann muss man Scheitelpunkte auf einer der anderen Achsen zu Hilfe nehmen: Mit Hife des Schiebereglers kann man den Scheitelpunkt auf der -Achse wählen. Besondere Quartiken sind diejenigen, deren Scheitelpunkt mit einem der anderen Brennpunkte übereinstimmt. In der -Ebene könnte das die Quartik mit den Brennpunkten und dem Scheitelpunkt sein. Diese Kurven sind die Fokal-Kurven der Schar. Nähern die Scheitelpunkte sich einer solchen Lage, so entarten die Cycliden in flache Flächenstücke, deren Ränder die Fokal-Kurven sind. Die Koeffizienten dieser entarteten Cycliden werden mit den obigen Formeln berechnet, beispielsweise mit .
Sonderfälle: Wir haben die Gleichung im Applet nicht in der etwas allgemeineren Form
  • mit
verwendet, um die nötigen Fallunterscheidungen zu begrenzen.
  • : Quadriken mit 3 Symmetrie-Ebenen
  • : Quadriken invertiert
  • : 1-teilige Darboux-Cycliden
  • 2 der Koeffizienten sind gleich: Rotations-Symmetrie
  • Einer der Koeffizienten ist gleich 1 bzw. gleich -1: die Quartiken in den zugehörigen Ebenen zerfallen in elliptische Kreispaare (2 sich schneidende Kreise) bzw. in hyperbolische Kreispaare (ohne Schnittpunkte)
  • sind die verschiedenen Tori-Typen, erreicht man durch geeignete Streckung. Der Torus liegt dann symmetrisch zur Einheitskugel.
  • Möbius-transformierte der Dupinschen Cycliden: Zitat (wikipedia) "Jede Dupinsche Zyklide ist das Bild eines senkrechten Kreiszylinders oder eines senkrechten Kreiskegels oder eines Rotationstorus unter einer Inversion (Spiegelung an einer Kugel)."
Hinweise und Links: 1): Die Punkte des Möbiusraums kann man projektiv beschreiben in einem reellen 4-dimensionalen Raum mit nicht-ausgearteter Möbius-Quadrik der Signatur (+,+,+,+,-). Die Punkte des Möbiusraums sind dann die Punkte auf der Möbius-Quadrik. Eine Darboux Cyclide ist der Schnitt dieser Quadrik mit einer 2-ten Quadrik. Neben der Möbius-Form besitzt der zugehörige 5-dimensionale reelle Vektorraum eine 2-te symmetrische selbstadjungierte Bilinearform. Dazu sollte es mindestens einen Eigenvektor geben. 2): Die Eigenräume sind paarweise orthogonal bezüglich der Möbiusform, bestenfalls ergeben sich 5 paarweise orthogonale Symmetrie-Kugeln, welche als die 3 Koordinatenebenen, die Einheitskugel und eine dazu orthogonale imaginäre Kugel gewählt werden können.- 3): Obwohl im Handbuch zu lesen ist, dass geogebra komplexe Zahlen nicht unterstützt, kann man in geogebra ganz trefflich komplex rechnen. Die wichtigsten Funktionen (, sin, cos, exp, ln ...) können als komplexe Funktionen behandelt werden, Berechnungen lassen sich klaglos komplex durchführen! Z.B.: die Koeffizienten sind reell, die Zahlen ebenfalls, abgesehen vom Sonderfall , bei welchem die Cyclide rotationssymmetrisch ist und Brennpunkte zusammenfallen!! Die (reelle) Berechnung liefert in manchen Fällen wegen des bekannten Verhaltens der Wurzel-Funktion bei negativen Radikanten kein Ergebnis. Mit dem "Trick" rechnet in geogebra die Wurzel-Funktion komplex, und so werden in entsprechenden Fällen die Brennpunkte mit denselben Formeln komplex berechnet, wenn sie auf dem Einheitskreis liegen! 4): Zur Möbiusgeometrie: vgl. das geogebra-book Moebiusebene 5): Für 2-teilige bizirkulare Quartiken kennen wir Parameterdarstellungen

Darboux Cycliden_ Die Formeln - GeoGebra

Darboux Cycliden_ Die Formeln - GeoGebra.pdf

Darboux Cycliden_ Die Formeln - GeoGebra.pdf

Konfokale 2-teilige Darboux Cyclidenerstellt mit obigem Applet

New Resources

Discover Resources

Discover Topics