harmonische boventonen
waar komt welluidendheid vandaan?
De beoordeling die Pythagoras gaf aan de welluidendheid van samenklanken was helemaal geen kwestie van toevallige, persoonlijke voorkeur. Ze had alles te maken met harmonische boventonen.
Een orgelpijp, snaar of menselijke stem produceert immers nooit een klank van die ene frequentie. Je hoort steeds en mengeling van meerdere tonen. Samen bepalen ze de klankkleur.
Hier hoort wat fysica bij.
harmonische boventonen
Instrumenten produceren geen zuivere sinusfuncties. Steeds klinken zogenaamde harmonische tonen of boventonen mee. Wanneer een pijp van het orgel wordt aangeblazen, ontstaat geluid van diverse golflengtes. Maar alleen het geluid met een golflengte die past in de lengte die ter beschikking staat (orgelpijp, fluit, snaar…), kan blijven bestaan. De meest eenvoudige golf bepaalt de toonhoogte.
De andere tonen hoor je niet als aparte tonen maar als een integrerend deel van de grondtoon. In het geval van een gesloten pijp treedt er een staande golf op als de halve golflengte gelijk is aan de lengte van de pijp. Hoe langer de pijp, hoe langer de golf en hoe kleiner de frequentie: Langere orgelpijpen produceren dus lagere tonen dan kortere. Maar er is niet alleen die ene golf.
Ook golven waarbij de golflengte meerdere keren 'past' in de lengte van de pijp kunnen een staande golf
veroorzaken, zoals golflengten van 1x de lengte van de pijp, 2x de lengte van de pijp, etc.
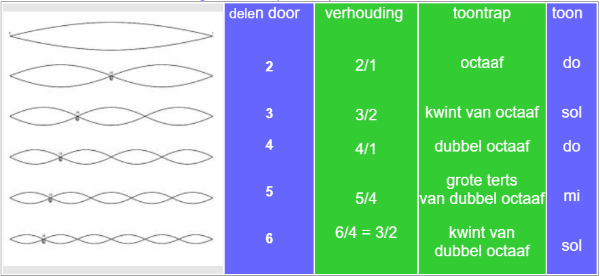
Wat zijn nu de frequentieverhoudingen van deze boventonen? We weten hierbij:
- een verhouding 2/1 bepaalt een octaaf (do - do)
- een verhouding 3/2 bepaalt een kwint (do - sol)
- een verhouding 5/4 bepaalt een grote terts (do - mi)
Versleep de schuifknop en verdeel de lengte
overzicht van de opeenvolgende boventonen
Wat kiest Pythagoras (en wij) eigenlijk
Pythagoras (en wij) geven bij een samenklank met een gegeven toon de een voorkeur aan tonen die in de reeks boventonen zitten van deze gegeven toon: octaven, kwinten en ook tertsen.
Een toonsysteem opbouwen met 3/2-verhoudingen is dus eigenlijk een logische keuze.
Omdat octaven en kwintverhoudingen prominent zijn in harmonische boventonen komen ze niet alleen voor in ons westers toonsysteem, maar ook in andere toonsystemen. Het verschil zit dat enkel in de beslissing welke tonen je naast octaaf en kwint nog opneemt en in hoeveel delen je een octaaf verdeelt.
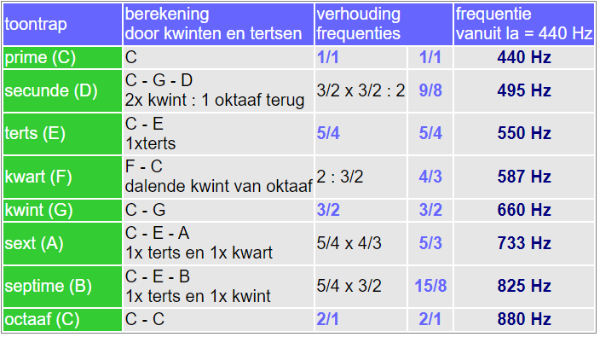
De reine stemming
Reeds rond 300 v.C werden alternatieven bedacht voor de stemming van Pythagoras.
De terts wordt niet meer berekend vanuit opeengestapelde kwinten maar rechtstreeks vanuit de verhouding 5/4.
Ook sext en septiem worden niet meer berekend vanuit de kwint, maar vanuit deze terts.
Waar blijft de gulden snede?
In klassieke toonsystemen wordt wereldwijd gekozen voor welluidendheid. Door het bestaan van harmonische toonverhoudingen vind je in toonsystemen enkel verhoudingen van gehele getallen terug.
Een gulden -verhouding (0.618) moet je hier niet zoeken.
Hoe het verhaal van ons westers toonsysteem verder loopt, kan je verder volgen op de pagina
van sinusfuncties tot een toonsysteem en volgende pagina's.