El número e
El “abuelo” de e fue John Napier, quien nació en 1550 en Edimburgo. Él fue el primero en definir y trabajar con los logaritmos (Mirifici Logarithmorum Canonis Descriptio, 1614) o números artificiales como los llamó, con lo cual se simplificaron los cálculos matemáticos y fue posible realizar otros, ya que las multiplicaciones se pueden sustituir por sumas, las divisiones por restas, las potencias por productos y las raíces por divisiones. La idea de Napier para concebir los logaritmos fue la comparación entre 2 progresiones, una aritmética y una geométrica. Años después fueron publicadas, en un apéndice al trabajo de Napier, unas tablas de logaritmos naturales de varios números pero en base e, aunque aún no se reconocía como una constante. El símbolo e hace su aparición en una carta que escribió Leonhard Euler a Goldbach en 1731. Euler realizó varios descubrimientos en torno a e y en 1748 publicó su obra Introductio in analysin infinitorum.
Proporcionó un análisis completo y demostró que: e = 2.7182818284590452e puede ser definido de manera algebraica mediante fracciones continuas que es lo que expresó Euler, pero también puede ser representado como una serie infinita
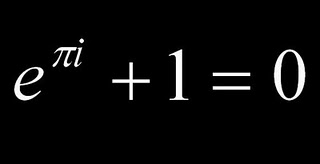
07
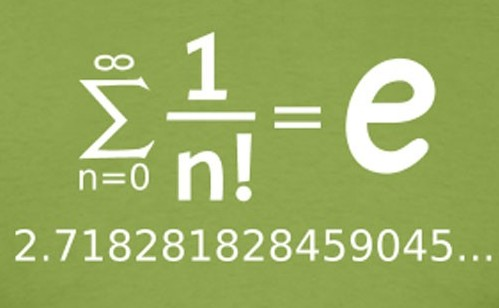
¿Cuál es el nombre correcto del país que habitamos?
De la fórmula general para ecuaciones de segundo grado ¿cual es la expresión denominada discriminante?

