Congruencia de Triángulos: Criterio LLL
Concepto
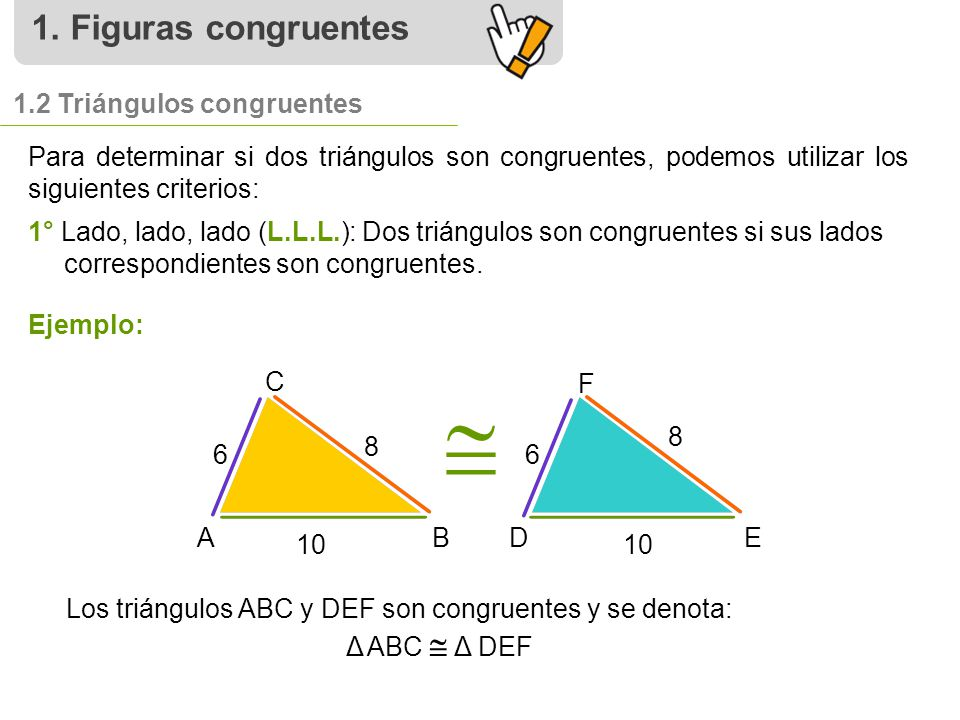
En matemáticas, dos figuras de puntos son congruentes si tienen los lados iguales y el mismo tamaño (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es combinación de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes. Criterios de congruencia de triángulos: Los criterios de congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos. Primer criterio de congruencia: LLL Dos triángulos son congruentes si sus tres lados son respectivamente iguales. a ≡ a’ b ≡ b’ c ≡ c’ → triáng ABC ≡ triáng A’B'C’ Segundo criterio de congruencia: LAL Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos. b ≡ b’ c ≡ c’ α ≡ α’ → triáng ABC ≡ triáng A’B'C’ Tercer criterio de congruencia: ALA Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado. b ≡ b’ α ≡ α’ β ≡ β’ → triáng ABC ≡ triáng A’B'C’
Construcción de Triángulos Congruentes
Construcción de Triángulos Congruentes