Ejercicio. Parametrización de una curva.
Algunos carnavales tienen una versión de una noria doble. Un largo brazo central gira en el sentido de las manecillas del reloj. En cada extremo del brazo central hay una noria que gira en sentido de las manecillas del reloj al rededor del brazo central. Asumimos que el largo del brazo central es de 200 pies y gira sobre su centro. Asumimos también que las norias tienen un radio de 40 pies y giran a la misma velocidad que el brazo central. Encuentre la ecuación paramétrica para la posición de un pasajero y grafique la su traza. Ajuste la velocidad de rotación de las norias para mejorar el viaje.
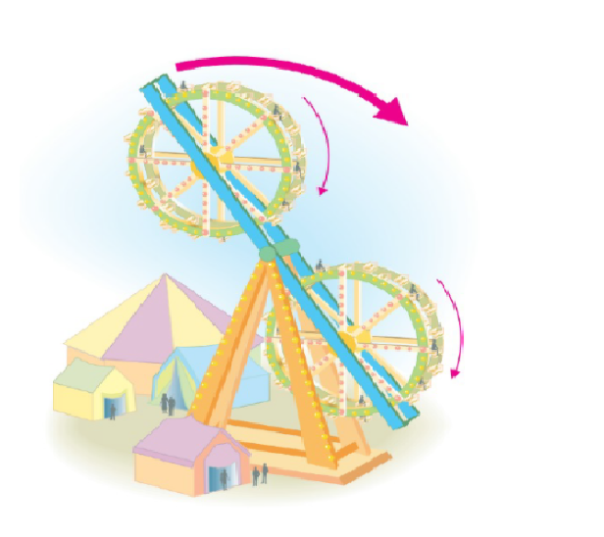
Comenzamos parametrizando el movimiento circular del brazo grande.
Dado que se trata de un movimiento, circular la parametrización bajo el parámetro es:
donde es el radio del círculo, en este caso, la mitad de la longitud del brazo grande: 100. Sin embargo, con esa parametrización la orientación de la curva es en sentido contrario a las manecillas del reloj. Con lo cual, la parametrización debe ser . Así, la dirección de la curva va en sentido de las manecillas del reloj.
Ahora consideremos que la noria que está en la punta del brazo. Pensemos por un momento, por simplicidad, que el brazo largo central está estático en . La parametrización del movimiento de la noria es igual a la del brazo central, pero desplazado hacia el inicio del brazo central, dado que se trata de un movimiento circular. Esta vez . Llamemos a la parametrización de este movimiento . Por lo tanto:
Si juntamos el movimiento al brazo central y el de la noria, obtenemos la curva que describe el movimiento del pasajero. La curva resultante es: .
El resultado es un movimiento circular de un radio mayor. Sin embargo, podemos ajustar la velocidad de ambos movimientos para lograr un movimiento más interesante. Por ejemplo, si la velocidad del brazo central es 5 veces más grande que la de la noria obtenemos el movimiento que se muestra a continuación:
Si la velocidad de la noria es 4 veces más grande que la del brazo central obtenemos el movimiento que se muestra a continuación: