Composición Aritmética. Theo Doesburg
Theo van Doesburg nació como Christiaan Emil Marie Küpper en Utrecht. Más tarde adoptó el apellido de su padrastro. A los 19 años comenzó a estudiar pintura. Además, se ganó la vida con el trabajo crítico de arte para una revista.
Durante su servicio militar en Tilburg en 1915, se encontró con una crítica de una exposición de Piet Mondrian . Juntos, los dos artistas fundaron la revista "De Stijl" en Leiden en 1917, desde la cual todo el movimiento artístico del mismo nombre asumió una "abstracción total".
La arquitectura y el arte deben combinarse, los elementos geométricos simplificados se convierten en su nuevo idioma.Van Doesburg dijo:
"Lo que la cruz representa para los primeros cristianos representa el cuadrado para nosotros, la plaza conquistará la cruz".
Sin embargo, la colaboración entre Van Doesburg y Mondrian en "De Stijl" más tarde fracasó en la cuestión de si se permitía el uso de diagonales en pinturas abstractas. Mientras que Van Doesburg lo defendió, Mondrian se opuso.
Paso a paso
Dibujamos dos puntos cualesquiera A y B.
Dibujamos el polígono regular de 4 lados generado por los puntos A y B. Lo renombramos como pol1
Con el botón
homotecia, generamos los puntos A', B' y C':
A'=Homotecia(A,2,D)
B'=Homotecia(B,2,D)
C'=Homotecia(C,2,D)
Generamos los puntos E y F escribiendo en la barra de entrada:
E= A' + 2/3 vector(A',B')
F= C'+ 2/3 vector(C',B')
Dibujamos el polígono regular de 4 lados generado por los puntos E y F. Lo renombramos como c1
homotecia, generamos los puntos A', B' y C':
A'=Homotecia(A,2,D)
B'=Homotecia(B,2,D)
C'=Homotecia(C,2,D)
Generamos los puntos E y F escribiendo en la barra de entrada:
E= A' + 2/3 vector(A',B')
F= C'+ 2/3 vector(C',B')
Dibujamos el polígono regular de 4 lados generado por los puntos E y F. Lo renombramos como c1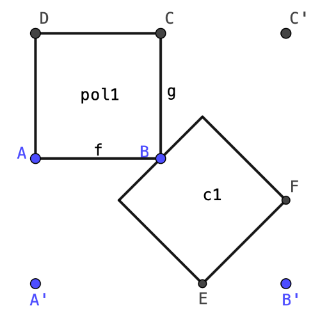
Ahora vamos a generar el cuadro usando el comando secuencia.
Creamos un deslizador de tipo entero entre 1 y 4. Lo renombrado como n.
Primero generamos los segmentos:
Secuencia(Homotecia( f,2^k,D),k,1,n+1)
Secuencia(Homotecia(g,2^k,D),k,1,n+1)
Secuencia(Homotecia(c1,2^k,D),k,1,n)
Secuencia(Homotecia(pol1,2^k,D),k,1,n)