Funciones
Funciones
Te invito a trabajar el tema de las funciones, y de manera específica la función lineal:
Recuerda que en esta sección repasamos los conceptos de función, dominio, codominio, imagen, anti-imagen y gráfica; ademas de que resolveremos uno que otro ejercicio:
FUNCIÓN
Definición:
Sean A y B conjuntos no vacíos. Una función de A en B es una relación que asigna a cada elemento x del conjunto A uno y solo un elemento y del conjunto B.
Se expresa como: f: A  B
X
B
X  f(x) = y
f(x) = y
 Dominio: es el conjunto de todos los valores para los cuales está definida la función y se denota Dom f.
Rango: es el conjunto de todos los valores que toma la variable dependiente (Y), y se denota Ran f.
Imagen es el valor que toma la variable y respecto a un valor determinado de la variable x.
La antiimagen es el valor que toma la variable x respecto a un valor que ha tomado la variable y.
Función Creciente: es aquella que al aumentar la variable independiente, también aumenta la variable dependiente.
Función Decreciente: es aquella que al aumentar la variable independiente, la variable dependiente disminuye.
Rango o Recorrido de f:
Es aquel subconjunto del codominio en el cual todos sus elementos son imagen de alguna preimagen del dominio o conjunto de partida. Se denota por R(f).
La función lineal
Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
Dominio: es el conjunto de todos los valores para los cuales está definida la función y se denota Dom f.
Rango: es el conjunto de todos los valores que toma la variable dependiente (Y), y se denota Ran f.
Imagen es el valor que toma la variable y respecto a un valor determinado de la variable x.
La antiimagen es el valor que toma la variable x respecto a un valor que ha tomado la variable y.
Función Creciente: es aquella que al aumentar la variable independiente, también aumenta la variable dependiente.
Función Decreciente: es aquella que al aumentar la variable independiente, la variable dependiente disminuye.
Rango o Recorrido de f:
Es aquel subconjunto del codominio en el cual todos sus elementos son imagen de alguna preimagen del dominio o conjunto de partida. Se denota por R(f).
La función lineal
Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
veamos el próximo vídeo
Analicemos el siguiente ejemplo:
Si el coste de fabricación de un bolígrafo es de 0,3$ por unidad y se venden por 0,5$, calcular:
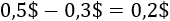 Por tanto, si se venden x bolígrafos, los beneficios son
Por tanto, si se venden x bolígrafos, los beneficios son
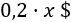 La función de beneficios es
La función de beneficios es
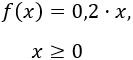 Exigimos x sea mayor o igual que 0 ( x ≥ 0x ≥ 0 ) porque el número de bolígrafos vendidos no puede ser negativo.Para representar la gráfica, damos algunos valores a xx para obtener algunos puntos:
Exigimos x sea mayor o igual que 0 ( x ≥ 0x ≥ 0 ) porque el número de bolígrafos vendidos no puede ser negativo.Para representar la gráfica, damos algunos valores a xx para obtener algunos puntos:
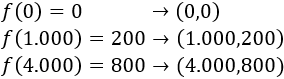 y la grafica de la función es:
y la grafica de la función es:
 Apartado b:
Si se venden 5.000 bolígrafos, aplicando la función, los beneficios son
Apartado b:
Si se venden 5.000 bolígrafos, aplicando la función, los beneficios son
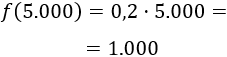 Los beneficios son 1.000$.
Apartado c:
Queremos calcular el número xx de bolígrafos vendidos para que las ganancias sean 1.648$.
Para ello, resolvemos la ecuación
Los beneficios son 1.000$.
Apartado c:
Queremos calcular el número xx de bolígrafos vendidos para que las ganancias sean 1.648$.
Para ello, resolvemos la ecuación
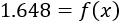 Es decir,
Es decir,
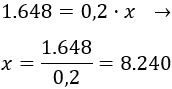 Deben venderse 8.240 bolígrafos.
Deben venderse 8.240 bolígrafos.
- La función de beneficios en función del número de bolígrafos vendidos. Representar su gráfica.
- Calcular los beneficios si se venden 5.000 bolígrafos.
- Calcular cuántos bolígrafos deben venderse para generar unos beneficios de 1.648$.
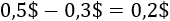 Por tanto, si se venden x bolígrafos, los beneficios son
Por tanto, si se venden x bolígrafos, los beneficios son
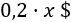 La función de beneficios es
La función de beneficios es
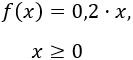 Exigimos x sea mayor o igual que 0 ( x ≥ 0x ≥ 0 ) porque el número de bolígrafos vendidos no puede ser negativo.Para representar la gráfica, damos algunos valores a xx para obtener algunos puntos:
Exigimos x sea mayor o igual que 0 ( x ≥ 0x ≥ 0 ) porque el número de bolígrafos vendidos no puede ser negativo.Para representar la gráfica, damos algunos valores a xx para obtener algunos puntos:
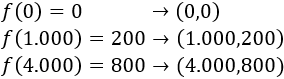 y la grafica de la función es:
y la grafica de la función es:
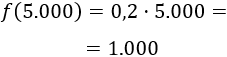 Los beneficios son 1.000$.
Apartado c:
Queremos calcular el número xx de bolígrafos vendidos para que las ganancias sean 1.648$.
Para ello, resolvemos la ecuación
Los beneficios son 1.000$.
Apartado c:
Queremos calcular el número xx de bolígrafos vendidos para que las ganancias sean 1.648$.
Para ello, resolvemos la ecuación
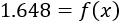 Es decir,
Es decir,
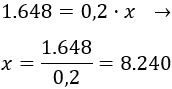 Deben venderse 8.240 bolígrafos.
Deben venderse 8.240 bolígrafos.
Marilenny - Función lineal (Material para estudio)
Función lineal ( Aplicaciones)
Resolvamos el siguiente ejercicio:
1. Un algodonero recoge 30 Kg cada hora, y demora media hora preparándose todos los días cuando inicia la jornada. La función lineal que representa esta situación es y = 30x – 15 donde y representa los Kg de algodón recogido y x el tiempo transcurrido en horas.
Realiza una tabla para la anterior función y grafícala.
¿Cuántos Kg de algodón se recogerán en una jornada de 8 horas?
Solución:
Primero realizamos la tabla.
y luego graficamos:
Y (Kg algodón) | X (Tiempo en horas)
|
| 0.5 | 0 |
| 1 | 15 |
| 1.5 | 30 |
| 2 | 45 |
otra gráfica de la función es:
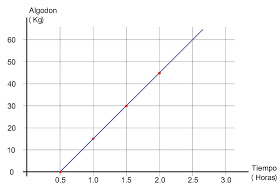
Ahora para saber cuanto algodón se recoge en 8 horas:
y = 30x – 15 para x = 8 necesitamos hallar el valor de y para eso remplazamos a la x por su valor que es 8 y nos queda
y = 30(8) – 15 = 240 - 15 = 225 (recuerda que 30(8) es un producto)
y = 225 Kg
La cantidad de algodón recogido en ocho horas es de 225 kg
Si tienes problemas para realizar la tabla repasa los vídeos :
