Umfang & Flächeninhalt vom Kreis - Unterrichtsplanung
Kurzinformation
- Thema: Umfang und Flächeninhalt eines Kreises
- 8. Schulstufe, Mathematik
- Dauer: 3 EH
- SchülerInnenmaterial
- Spezielle Materialien: Schnur (sollte nicht leicht dehnbar sein), Lineal, Kreisflächen aus Karton (auch runde Gegenstände sind möglich: z.B. Yoghurt Becher, Vase, Glas,...), Geogebra (Laptop, Computer)
Vorwissen und Voraussetzungen
Die SchülerInnen wissen...
- ... wie man den Umfang und Flächeninhalt von Rechtecken, Quadraten und Dreiecken berechnet…
- ... wie man Formeln umformt
Lernergebnisse und Kompetenzen
Die SchülerInnen können...
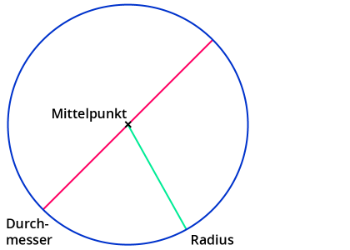
- ... einen Kreis beschriften und einzeichnen (Mittelpunkt, Durchmesser, Radius).
- ... den Zusammenhang zwischen Umfang/Fläche und Durchmesser bzw. zwischen Umfang/Fläche und Radius verstehen.
- ... Berechnungen zu Umfang und Flächeninhalt des Kreises durchführen.
Unterrichtsablauf
1. Einheit: Zuerst wird der Kreis allgemein eingeführt. Danach folgt eine Gruppenarbeit zur Erarbeitung der Formel für den Umfang. Mit einem Arbeitsblatt wird die Formel angewendet und geübt.
2. & 3. Einheit: Das Arbeitsblatt wird fertig gemacht und mit der Klasse verglichen.
In Gruppen wird die Formel für den Flächeninhalt erarbeitet. Dann wird zur zusätzlichen Darstellung ein Geogebra Applet verwendet. Zur Übung und zur Sicherung der Formeln für Umfang und Flächeninhalt wird ein 2. Arbeitsblatt mit Rechenaufgaben verwendet.
Einführung (ca. 10 Minuten)
Der Kreis wird kurz mittels Skizze eingeführt (Kreislinie, Radius, Durchmesser, Mittelpunkt).
Gruppenarbeit- Erarbeitung Umfang (ca. 20 Minuten)
In 4er Gruppen bekommen die SchülerInnen eine Schnur und einen Kreis aus Karton. Davon sollen sie den Durchmesser und de Umfang des Kreises abmessen. Alternativ können auch andere Gegenstände mit runder Fläche gemessen werden (z.B. Vase, Teller, Tasse, ...).
Anschließend bekommen die SchülerInnen den Auftrag ihren gemessenen Umfang durch den gemessenen Durchmesser zu dividieren. Die Ergebnisse jeder Gruppe werden an der Tafel festgehalten.
Erklärung, Übung (ca. 20 Minuten)
Die Zahl Pi wird kurz eingeführt und die Formel für den Umfang eines Kreises wird erarbeitet.
Anschließend werden einfache Beispiele zur Berechnung des Umfangs bei gegebenen Radius bzw. Durchmesser gemeinsam gerechnet.
Danach bekommen die SchülerInnen ein Ar
beitsblatt, welches sie mit ihrem Sitznachbarn gemeinsam lösen.Gruppenarbeit: Erarbeitung Flächeninhalt
Die SchülerInnen bekommen in 3er oder 4er Gruppen den Auftrag, den Flächeninhalt des Kreises zu bestimmen.
Anschließend können die SchülerInnen den Geogebra Link ausprobieren, oder es wird von der Lehrperson hergezeigt. Die allgemeine Herleitung der Flächeninhaltsformel wird nochmals an der Tafel erklärt.
Übung
Die SchülerInnen sollen den Übungszettel alleine oder zu 2. lösen. Hier sind Beispiele zu Umfang und Flächeninhalt zu rechnen.
Sicherung / Hausübung
Wenn die SchülerInnen mit dem Übungszettel nicht fertig werden, kann dieser als Hausübung gegeben werden.
Überprüfen des Lernerfolges
Während der Unterrichtseinheit kann man die Mitarbeit der einzelnen SchülerInnen überprüfen,
indem man schaut, ob sie sich im Unterricht einbringen bzw. die Beispiele lösen
können.
Lösungen
Links zu Materialien und Quellen
Materialien
Quellen:
Schulbuch: mathematiX 4Mathematik lehren 2018 Band 208
Mathematik lehren 1999 Band 93
Mathematik lehren 2003 Band 121
